 Problem K. 229. (December 2009)
Problem K. 229. (December 2009)
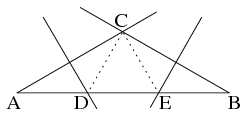
K. 229. Show that a given line segment AB can be divided into three equal parts by the following method: A 30o angle is drawn to each end of the line segment so that their other arms intersect at point C. Then the perpendicular bisectors of the line segments AC and BC are constructed. These will intersect AB at two points that cut it into three equal parts.
(6 pont)
Deadline expired on January 11, 2010.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Az ábrán a kérdéses pontokat \(\displaystyle D\)-vel és \(\displaystyle E\)-vel jelöltük.
Mivel \(\displaystyle D\) a felezőmerőleges pontja, ezért \(\displaystyle AD=CD\). Hasonlóan \(\displaystyle BE=CE\). Ekkor nem csak \(\displaystyle A\)-nál és \(\displaystyle B\)-nél van \(\displaystyle 30^\circ\), hanem \(\displaystyle ACD\angle\) és \(\displaystyle BCE\angle\) is \(\displaystyle 30^\circ\)-os, ami alapján belátható, hogy \(\displaystyle CDE\) háromszög minden szöge \(\displaystyle 60^\circ\), azaz szabályos. Ez azt is jelenti, hogy valóban \(\displaystyle AD=DE=EB\).
Statistics:
167 students sent a solution. 6 points: 57 students. 5 points: 34 students. 4 points: 25 students. 3 points: 16 students. 2 points: 13 students. 1 point: 8 students. 0 point: 12 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, December 2009
