 Problem K. 248. (March 2010)
Problem K. 248. (March 2010)
K. 248. The diagram shows a net of a cube. In how many different ways is it possible to colour two of the six squares red, and the other four with four different colours: white, green, yellow and blue, so that the resulting cube does not have two adjacent faces of the same colour?
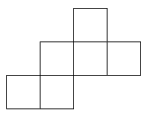
(6 pont)
Deadline expired on April 12, 2010.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Számozzuk meg a négyzeteket!
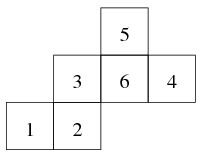
Az összehajtás után az 1-nek a 6, a 6-nak az 1 kivételével mindegyik a szomszédja lesz; a 2-nek az 5, az 5-nek a 2 kivételével mindegyik a szomszédja lesz; a 3-nak a 4, a 4-nek a 3 kivételével mindegyik a szomszédja lesz. Pirosra tehát csak az 1-6, 2-5 vagy 3-4 oldalakat festhetjük, így a piros lapok elhelyezésére három lehetőség adódik. Bármelyik párost választjuk pirosnak, akkor a megmaradt négy négyzetet 24 különböző módon tudjuk kifesteni. Vagyis 72 különböző módon színezhető a feltételeknek megfelelő módon az ábra.
Statistics:
133 students sent a solution. 6 points: 78 students. 5 points: 31 students. 4 points: 6 students. 3 points: 4 students. 2 points: 7 students. 1 point: 2 students. Unfair, not evaluated: 5 solutionss.
Problems in Mathematics of KöMaL, March 2010
