 Problem K. 251. (March 2010)
Problem K. 251. (March 2010)
K. 251. Extend each diagonal of a square of side in one direction by the length of the side.
a) How long is the line segment connecting the new endpoints of the extensions?
b) Show that there is a vertex of the square that forms an isosceles triangle with the new endpoints of the extensions.
(6 pont)
Deadline expired on April 12, 2010.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Használjuk az ábra jelöléseit.
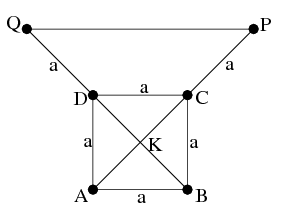
\(\displaystyle a)\) Tudjuk, hogy \(\displaystyle AC=\sqrt 2 a\), ezért \(\displaystyle KP= \left (\frac{\sqrt 2}{2} + 1 \right )a\). Mivel \(\displaystyle KPQ\) egyenlőszárú derékszögű háromszög, ezért \(\displaystyle QP=\sqrt 2 \left( \frac{\sqrt 2}{2} + 1\right)a = (\sqrt 2 +1)a\). Tudjuk, hogy \(\displaystyle a=\sqrt 2 -1\), így a keresett távolság: \(\displaystyle QP= (\sqrt 2 +1)(\sqrt 2 -1)=1\).
\(\displaystyle b)\) Mivel \(\displaystyle AP=\sqrt 2 a + a =(\sqrt 2 +1)a= (\sqrt 2 +1)(\sqrt 2 -1)=1\), ezért \(\displaystyle AP=QP\), vagyis \(\displaystyle AQP\) egyenlőszárú háromszög. (Természetesen a szimmetria miatt \(\displaystyle BPQ\) is egyenlőszárú háromszög.)
Statistics:
120 students sent a solution. 6 points: Békési Zsuzsanna, Bingler Arnold, Bogye Balázs, Csapodi Borbála, Csóka József, Dankovics Viktor, Déri Tamás, Dóka Tamás, Domján Júlia, Drávay Zorka, Erdélyi Vivien, Erdős Szilvia, Frank Evelyn, Fülep Andrea , Girst Gábor, Hopp Norbert, Károly Péter Balázs, Katona 100 Bálint, Kedves Máté, Kelemen Bendegúz, Kertész Dávid, Keszthelyi Gergely, Leitereg András, Marx Anita, Matos Bence, Mezősi Máté, Molnár 918 Nóra, Molnár Ákos, Müller Dóra Tímea, Nagy 021 Tibor, Nagy 224 Réka, Pintér 403 Gabriella, Sárközy Kristóf, Serfőző Lőrinc, Szabó 262 Lóránt, Szentgyörgyi 994 Rita, Szeredi Levente Soma, Szilágyi Gergely Bence, Szkalisity Ábel, Takács 737 Gábor, Tóth 315 Benedek, Tóth Endre, Tóth Márton, Turányi László, Vecsernyés Tamás, Végh Dávid András, Welsz Ágnes, Wiandt Zsófia. 5 points: 31 students. 4 points: 15 students. 3 points: 10 students. 2 points: 4 students. 1 point: 6 students. 0 point: 3 students. Unfair, not evaluated: 3 solutionss.
Problems in Mathematics of KöMaL, March 2010
