Problem K. 259. (October 2010)

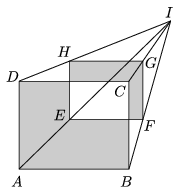
K. 259. ABCD and EFGH are coplanar rectangles with parallel sides. Given that AB=15 cm, AD=12 cm, EF=10 cm, EH=8 cm, FI=14 cm, calculate the difference of the shaded areas.

(6 pont)

Deadline expired on November 10, 2010.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Az \(\displaystyle ABCD\) téglalap satírozott részének területét jelölje \(\displaystyle T_s\), az \(\displaystyle EFGH\) téglalap satírozott részének területét pedig \(\displaystyle t\). A téglalapok közös része szintén téglalap, melynek területe \(\displaystyle \tau\). Ekkor \(\displaystyle T-t=T+\tau -\tau -t=T_{ABCD}-T_{EFGH}=15\cdot 12 -10\cdot 8=80\). A satírozott síkidokok területének különbsége 80.

Statistics:

218 students sent a solution.
6 points:	134 students.
5 points:	37 students.
4 points:	8 students.
3 points:	8 students.
2 points:	9 students.
1 point:	5 students.
0 point:	7 students.
Unfair, not evaluated:	10 solutionss.

Problems in Mathematics of KöMaL, October 2010