Problem K. 262. (October 2010)

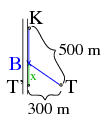
K. 262. The entrance to the Happy Holidays Campsite lies right next to a straight road. The entrance to the Sweet Summer Youth Camp lies 300 metres off the road. The distance between the two entrances is 500 as the crow flies. A restaurant is to be built right next to the road. Where should it be built so that it is equidistant from the entrances of the campsite and the youth camp?

(6 pont)

Deadline expired on November 10, 2010.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A kemping bejáratát jelöljük \(\displaystyle K\)-val, a tábor bejáratát \(\displaystyle T\)-vel, az út azon pontját, ami legközelebb van \(\displaystyle T\)-hez \(\displaystyle T\ '\)-vel, a büfé helyét pedig \(\displaystyle B\)-vel egy térképen. \(\displaystyle KT\ 'T\) derékszögű háromszöget alkot, Pithagorasz tétele szerint \(\displaystyle KT\ '=\sqrt{500^2-300^2}=400\). A feladat szerint \(\displaystyle KB=BT\), továbbá legyen \(\displaystyle BT\ '=x\) (\(\displaystyle x<400\), megengedve, hogy x<0 esetén \(\displaystyle B\)-t és \(\displaystyle K\)-t a \(\displaystyle TT\ '\) egyenese által meghatározott különböző félsíkok tartalmazzák). Ekkor \(\displaystyle BT\ 'T\) derékszögű háromszögben Pithagorasz tétele szerint \(\displaystyle 400-x=KB=BT\sqrt{x^2+300^2}\). Az egyenlet két (pozitív) oldalának négyzetei \(\displaystyle 160000-800x+x^2=90000+x^2\), ahonnan \(\displaystyle x=87,5\). A büfét a kemping bejáratától 312,5 méterre a tábor felé kell megépíteni az út mellett.

Statistics:

340 students sent a solution.
6 points:	190 students.
5 points:	11 students.
4 points:	2 students.
3 points:	15 students.
2 points:	62 students.
1 point:	34 students.
0 point:	16 students.
Unfair, not evaluated:	10 solutionss.

Problems in Mathematics of KöMaL, October 2010