 Problem K. 278. (January 2011)
Problem K. 278. (January 2011)
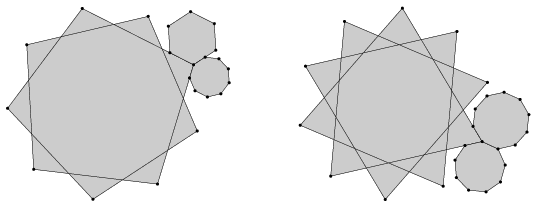
K. 278. Each of the two diagrams below shows three regular polygons (some of which are stellated polygons) that meet at a vertex. Do they really touch each other along their sides in both cases, or is there a diagram that ``lies''?
(6 pont)
Deadline expired on February 10, 2011.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Az első ábrában a csillag-kilenc-szög oldalainak metszéspontjai egy szabályos kilencszöget alkotnak (forgás-szimmetria miatt), ezért az egymást metsző oldalak egymással \(\displaystyle 140^\circ\)-os szöget zárnak be. A csillagszög csúcsa és a vele szemközti oldalon levő két oldalmetszéspont alkotta háromszög szögei ezért \(\displaystyle 40^\circ, 40^\circ, 100^\circ\). A szabályos hatszög szögei \(\displaystyle 120^\circ\), továbbá a szabályos kilencszög szögei \(\displaystyle 140^\circ\). A közös csúcsban egymáshoz csatlakoztatva sorban a sokszögek oldalait egy szögtartományt határoznak meg. Ha ez a szög teljes szög, akkor az ábra nem csal. Mivel \(\displaystyle 100^\circ+120^\circ+140^\circ=360^\circ\), ezért az első ábra nem csal.
A második ábrán egy csillag-tízszöget használtak. Az oldalak metszéspontjai közül az a 10, mely a sokszög középpontjához legközelebb van, egy szabályos tízszöget alkot, melynek szögei \(\displaystyle 144^\circ\). Ezen tízszög oldalegyenesei tehát \(\displaystyle 36^\circ\)-os szöget zárnak be egymással. Egy oldalegyenes és az őt \(\displaystyle 36^\circ\)-ban metsző két másik oldal alkotta háromszög harmadik szöge ezért \(\displaystyle 108^\circ\). (Ezen oldalak metszéspontjai, melyek távolab vannak a szabályos tízszöget alkotóknál, de közelebb, mint az eredeti csillagtízszög csúcsai egy csillagtízszöget alkotnak \(\displaystyle 108^\circ\)-os szögekkel.) Az eredeti csillagtízszög egy csúcsával szemközti két oldal és a csúcsból induló két oldal egy deltoidot határoznak meg, melynek három szöge ismert: \(\displaystyle 144^\circ, 72^\circ, 72^\circ\). Ezért az eredeti csillagtízszög szöge \(\displaystyle 72^\circ\). A szabályos tízszög szöge \(\displaystyle 144^\circ\), a szabályos kilencszög szöge pedig \(\displaystyle 140^\circ\). Összegük \(\displaystyle 366^\circ\), ami több, mint egy teljes szög, ezért az ábra csal, mert egy csúcs mentén egymás után illesztve a sokszögeket egymásba fognak lógni.
Statistics:
164 students sent a solution. 6 points: 100 students. 5 points: 23 students. 4 points: 21 students. 3 points: 5 students. 1 point: 3 students. 0 point: 5 students. Unfair, not evaluated: 7 solutionss.
Problems in Mathematics of KöMaL, January 2011
