 Problem K. 286. (February 2011)
Problem K. 286. (February 2011)
K. 286. There is a dwarf standing on each field of a 3×3 board. 2 of the dwarfs are liars. The liars never tell the truth. The other 7 dwarfs always tell the truth. Each dwarf is asked how many of the ones standing on fields adjacent to his field tell the truth. (Adjacent fields have an edge in common.) The answers are shown in the table. (For simplicity, the rows and columns of the board are denoted by letters and numbers.) What may be the positions of the liars on the board?
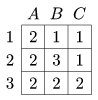
(6 pont)
Deadline expired on March 10, 2011.
Sorry, the solution is available only in Hungarian. Google translation
1. megoldás. Kezdjük el A1 mezőnél, és tegyük fel, hogy az ott álló törpe igazmondó. Ezen feltételezés alapján A2 és B1 helyeken is igazmondó áll. Mivel B1 szomszédai közül csak egy igazmondó, ezért B2 és C1 helyeken hazugok állhatnak. Így A2 mellett csak A3 helyen, mellette B3 helyen, ami mellett C3 helyen majd C2 helyen áll igazmondó törpe. Másrészről C1 hely mellett 2, B2 mellett 4 igazmondó áll, tehát tényleg hazudósak az ott álló törpék. Ha A1 helyen hazudós törpe áll, akkor valamelyik szomszédja is hazudós. A2 nem lehet hazudós, mert ha az lenne, akkor még egy másik szomszédjának is hazudósnak kellene lennie. Ha B1-n is hazudós áll, akkor minden további mezőn igazmondónak kell lennie a feladat szerint. Ebben az esetben a C2-n álló törpének 3 igazmondó szomszédja van és nem 1, így biztosan nem így helyezkedtek el a törpék.
2. megoldás. Nézzük meg, hogy egy hazudós törpe jelenléte hogyan befolyásolja az igazmondó szomszédok számát. Ha nem lenne hazudós, akkor a mezőkbe a szomszédok számát írtuk volna: a 9 szám összege pedig 24 lenne. Ha igazmondó áll egy hazudós mellett, akkor az igazmondó 1-gyel kevesebbet mond, mint az összes szomszédjának száma. Ha két hazudós egymás mellett áll, akkor ők vagy az összes szomszédaik számát mondják, vagy kettővel kevesebbet. Az A1, C1, A3, C3 mezőket nevezzük csúcsoknak (c), melyeknek 2 szomszédjuk van; az A2, B1, C2, B3 mezőket éleknek (e), melyeknek 3 szomszédjuk van és végül B2 legyen középen (k) 4 szomszéddal. Ha a két hazudós egymás mellett áll, akkor a szomszédok (igazmondók) 1-gyel kevesebbet mondanak, ők vagy a szomszédok számát vagy kettővel kevesebbet. Így ha (c)(e)-n áll hazudós akkor legfeljebb 7-tel, ha (k)(e)-n áll hazudós , akkor legfeljebb 9-cel mondanak kevesebbet a csupa igazmondókhoz képest. A feladatbeli táblázatban a számok összege 16, ami 8-cal kevesebb a 24-nél, tehát (c)(e) hazudós pár nem fordulhat elő. Ugyanakkor az sem lehet, hogy középen és valamelyik szomszédoson álljon hazudós, mert akkor a feladat szerint a középen álló igazat mond. tehát csak az történhetett, hogy középen és az egyik csúcsban áll hazudós törpe. Mivel ekkor az éleken igazmondóak állnak, ezért következik, hogy C1 csúcsban áll hazudós.
Statistics:
167 students sent a solution. 6 points: 90 students. 5 points: 7 students. 4 points: 38 students. 3 points: 17 students. 2 points: 12 students. Unfair, not evaluated: 3 solutionss.
Problems in Mathematics of KöMaL, February 2011
