 Problem K. 297. (September 2011)
Problem K. 297. (September 2011)
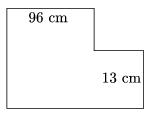
K. 297. A square is cut out of the upper right corner of the rectangle in the diagram. The area of the resulting figure is 2011 cm2. What was the area of the original rectangle?
(6 pont)
Deadline expired on October 10, 2011.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A kivágott négyzet oldalának hosszát jelöljük \(\displaystyle x\)-szel. Ekkor a síkidom területére fennáll, hogy \(\displaystyle (96+x)(13+x)-x^2=2011\). Rendezés után \(\displaystyle 109x=763\), ahonnan \(\displaystyle x=7\). Ennek segítségével az eredeti téglalap területe \(\displaystyle (96+7)(13+7)=2060\) \(\displaystyle cm^2\).
Statistics:
340 students sent a solution. 6 points: 302 students. 5 points: 4 students. 4 points: 1 student. 2 points: 3 students. 1 point: 7 students. 0 point: 22 students. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, September 2011
