 Problem K. 303. (October 2011)
Problem K. 303. (October 2011)
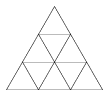
K. 303. How many triangles, rhombuses and cyclic trapeziums are there in the diagram?
(6 pont)
Deadline expired on November 10, 2011.
Sorry, the solution is available only in Hungarian. Google translation
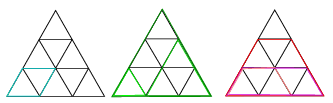
Megoldás. Rombuszból csak egyféle van (l. ábra): összesen 9 db található belőle az ábrán (az alsó sorban kettő balra, kettő jobbra fordulva, ugyanez minden oldalon, de a csúcsoknál levőket kétszer számoltuk, így 12–3=9 a teljes darabszám).
Háromszögből háromféle van, a legkisebből 9 db, a közepes méretűből 3 db, a legnagyobból pedig 1 db van, összesen 13 db.
Trapézból is háromféle van: a legkisebből 12 db van (egy oldallal párhuzamos alapokkal rendelkezőből az oldalon van három: kettő az ábrán látható helyzetben, egy pedig fejjel lefelé, és a középső sorban is van egy talpon állva), a közepes és a nagy méretűből is összesen 3-3 db van, összesen 18 db.
Tehát trapézból van a legtöbb.
Statistics:
331 students sent a solution. 6 points: 88 students. 5 points: 13 students. 4 points: 102 students. 3 points: 29 students. 2 points: 66 students. 1 point: 21 students. 0 point: 7 students. Unfair, not evaluated: 5 solutionss.
Problems in Mathematics of KöMaL, October 2011
