Problem K. 304. (October 2011)

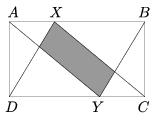
K. 304. Points X and Y divide the sides AB and CD, respectively, of a rectangle ABCD in a 1:2 ratio, as shown in the figure. What is the ratio of the areas of the grey quadrilateral and the rectangle ABCD?

(6 pont)

Deadline expired on November 10, 2011.

Sorry, the solution is available only in Hungarian. Google translation

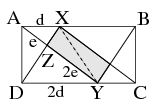
Megoldás. Az ábra szimmetriája miatt a satírozott négyszög paralelogramma. Rajzoljuk be ennek \(\displaystyle XY\) átlóját! Ez az átló felezi a paralelogramma területét. Az \(\displaystyle AXY\) háromszög területe az \(\displaystyle ABCD\) téglalap területének hatodrésze (alapja az \(\displaystyle AB\) harmadrésze, magassága \(\displaystyle BC\)). A \(\displaystyle DYZ\) háromszög oldalai kétszer akkorák, mint az \(\displaystyle AXZ\) háromszögé, mert a két háromszög hasonló. Így \(\displaystyle Z\) az \(\displaystyle AY\) szakasz harmadolópontja, ezért az \(\displaystyle XYZ\) háromszög területe az \(\displaystyle AXY\) háromszög területének kétharmada. Tehát az \(\displaystyle XYZ\) háromszög területe a téglalap területének hatodának kétharmada, azaz egykilencede. A paralelogramma területe ennek kétszerese, vagyis a téglalap területének 2/9 része.

Statistics:

207 students sent a solution.
6 points:	88 students.
5 points:	47 students.
4 points:	23 students.
3 points:	4 students.
2 points:	8 students.
1 point:	13 students.
0 point:	21 students.
Unfair, not evaluated:	3 solutionss.

Problems in Mathematics of KöMaL, October 2011