 Problem K. 305. (October 2011)
Problem K. 305. (October 2011)
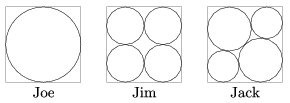
K. 305. Satellite pictures of some dry regions of the United States show interesting circular features. (E.g. to view the area of ZIP code 79068 in Texas, enter TX 79068 for search in Google Earth.) The circles are formed owing to an irrigation technology involving a long rod revolving about its midpoint or an endpoint. Since the water does not reach the entire area of the field, only the interior of the circles, part of the field will not have plants growing on it. Three brothers, Joe, Jim and Jack each have a square field 1 km on a side. The irrigated areas on their fields are laid out as shown in the figure. In Jack's arrangement, the radius of the smaller circles is 210.5 m. Which of the brothers has the most productive arrangement of circles on his field, that is, which of them can use the greatest fraction of his field for growing plants?
(6 pont)
Deadline expired on November 10, 2011.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Joe öntözőkörének sugara \(\displaystyle 500\ m\), így ő \(\displaystyle 500^2\cdot \pi \approx 785398\ m^2\) nagyságú területet tud öntözni és termelni rajta. Jim egy öntözőkörének sugara \(\displaystyle 250\ m\), de négy van belőle, ezért az által öntözött terület nagysága \(\displaystyle 4 \cdot 250^2\cdot \pi \approx 785398\ m^2\), megegyezik Joe-éval. Jack nagyobbik körének sugarát az alábbi ábra alapján számíthatjuk ki, felhasználva, hogy a négyzet átlójának hossza \(\displaystyle \sqrt 2\)-ször annyi, mint az oldalának hossza:
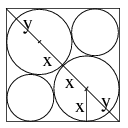
Jelölje \(\displaystyle x\) a nagyobbik kör sugarát. A nagy négyzet átlója \(\displaystyle 2x+2y\), ahol \(\displaystyle y=\sqrt 2 x\) (mert \(\displaystyle y\) az \(\displaystyle x\) oldalú négyzet átlója), azaz \(\displaystyle x = \frac{1000\sqrt 2}{2\sqrt 2 +2}\approx 292,9\ m\). A négy kör együttes területe: \(\displaystyle 2\cdot 292,9^2\cdot \pi+2\cdot 210,5^2\cdot \pi \approx 817 032\ m^2\). Tehát Jack elrendezése a leggazdaságosabb hármójuké közül.
Megjegyzés: A műholdas képeken nem látunk olyan elrendezést, mint Jacké, és a körök is nagyjából egyformának tűnnek. Lehet, hogy a gyártók csak egységes méretben gyártják az öntöző berendezéseket, de az is lehet, hogy még senkinek nem jutott eszébe változatni.
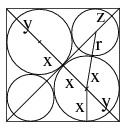
(A kisebbik kör sugarához az ábrán középen látható derékszögű háromszöget használhatjuk fel. Ha a kis kör sugarát \(\displaystyle r\) jelöli, akkor az átfogó \(\displaystyle x+r\), a befogók \(\displaystyle x\) és \(\displaystyle \frac{1000\sqrt 2}{2}-z\), ahol \(\displaystyle z=\sqrt 2 r\). Felírva a Pitagorasz-tételt \(\displaystyle x^2 + (500\sqrt 2 -r\sqrt 2)^2 = (x+r)^2\), behelyettesítve és a kapott másodfokú egyenletet megoldva \(\displaystyle r \approx 210,5\ m\).)
Statistics:
284 students sent a solution. 6 points: 90 students. 5 points: 20 students. 4 points: 7 students. 3 points: 6 students. 2 points: 132 students. 1 point: 17 students. 0 point: 9 students. Unfair, not evaluated: 3 solutionss.
Problems in Mathematics of KöMaL, October 2011
