Problem K. 306. (October 2011)

K. 306. A 4×4-es square table is filled in with the digits of 2011, so that each row, column and diagonal contains 2, 0, 1, 1 in some order. In how many different ways is that possible?

(6 pont)

Deadline expired on November 10, 2011.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Ha találunk egy megoldást, akkor annak elforgatottja és tükrözöttje is megfelelő lesz. Emiatt a bal felső sarokból induló átlóban levő 2-es pozíciójára csak két esetet kell vizsgálnunk: amikor a sarokmezőn áll, és amikor nem ott. Ha ebben az átlóban a 2-es a sarokban áll, akkor a másik átlóban levő 2-es nem lehet a sarokban, mert egy oszlopban vagy sorban két 2-es lenne. Így a másik átlóban levő 2-es a közbülső mezők valamelyikén áll, de a tükrözés miatt elég megnéznünk, ha a második sorban van ez a 2-es. Ez a két szám a harmadik és negyedik sorban levő 2-esek helyét már egyértelműen meghatározza.

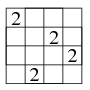
Mivel minden sorban, oszlopban és átlóban 0-ból is csak egy-egy darab van, ezért a 0-k alaphelyzete is ugyanez, ebből generálható a 0-k összes lehetséges elhelyezkedése (forgatással és tükrözéssel egymásba vihető összes lehetőség):

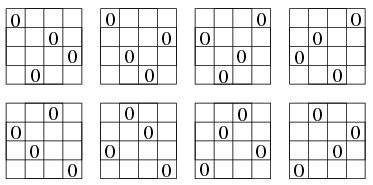
A kapott lehetőségeket összevetve a 2-esek elhelyezkedésével, összesen (a 2-esek rögzített helyzetéből kiindulva) három alapmegoldást kapunk:

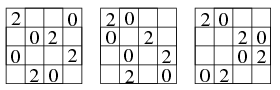
Az üres helyeket 1-esekkel megtöltve megkaptuk tehát az alapmegoldásokat. Ezek tükrözöttjei és elforgatottjai lesznek a megoldások. A bal felső sarokból induló átlóra tükrözéssel kapunk még egyet mindegyikből, majd a középpont körüli elforgatással mindezekből 3-3 új elrendezés adódik. Tehát a megoldások száma összesen 24. A korábban mondottak alapján ezen transzformációk útján kapottakon kívül más megoldás nincs.

Statistics:

224 students sent a solution.
6 points:	Belényesi Máté, Csilling Tamás, Czett Antal, Dombai Tamás, Fekete Panna, Gyuk Izabella, Holczer András, Jákli Aida Karolina, Jójárt Alexandra, Kling Anna, Korcsok Gergő Bence, Kovács 148 Dávid, Lengyel Ádám, Máté Bálint, Mészáros Gabriella, Olexó Tünde, Qian Lívia, Rózsa Alida, Szalai Norbert, Szalay Fanni, Sziegl Benedek, Tóth Adrián, Tóth László Gábor, Virágh Anna.
5 points:	Asbolt Máté, Balázs Bálint Bendegúz, Fülöp Erik, Görgei Anna Mária, Hegyi Zoltán, Iványi Blanka, Kocsis Gábor, Kondákor András, Markó Gergely, Molnár 286 Soma, Pap Olivér, Pásztor Adrienn, Pethő Luca, Porupsánszki István, Rátky Márton, Sorbán Zoltán, Székely Attila, Szigeti Gréta Anna, Sziklay Csenge, Tomku György.
4 points:	23 students.
3 points:	23 students.
2 points:	21 students.
1 point:	33 students.
0 point:	72 students.
Unfair, not evaluated:	8 solutionss.

Problems in Mathematics of KöMaL, October 2011