Problem K. 314. (December 2011)

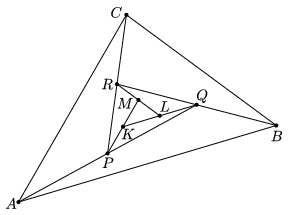
K. 314. The midpoint of the line segment AQ in the diagram is P, the midpoint of line segment BR is Q, the midpoint of CP is R, the midpoint of PL is K, and the midpoint of RM is L. Given that the area of triangle ABC is 441 cm², find the area of triangle KLM.

(6 pont)

Deadline expired on January 10, 2012.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Induljunk ki az \(\displaystyle PQR\) és \(\displaystyle KLM\) háromszögekből. A \(\displaystyle KLM\) és \(\displaystyle KRM\) háromszögek területe megegyezik, mert alapjuk (\(\displaystyle LM\) és \(\displaystyle RM\)) egyforma és ezekhez tartozó magasságuk is megegyezik. A \(\displaystyle KMR\) és \(\displaystyle KPR\) háromszögek területe is ugyanezen okok miatt egyenlő (\(\displaystyle KM=KP\) és ezekhez tartozó magasságuk közös). Hasonlóan, a háromszögeket kettesével tekintve (megrajzolva az \(\displaystyle RK\), a \(\displaystyle QM\) és a \(\displaystyle PL\) szakaszokat), belátható, hogy az ábrán így található 7 háromszög területe egyenlő; így a \(\displaystyle PQR\) háromszög területe a \(\displaystyle KLM\) háromszög területének hétszerese. Ugyanez a kapcsolat az \(\displaystyle ABC\) és a \(\displaystyle PQR\) háromszögek területe között is. Vagyis \(\displaystyle KLM\) területének \(\displaystyle 49\)-szerese az \(\displaystyle ABC\) területe. Tehát a kérdéses terület: \(\displaystyle 441 : 49 = 9 ~\text{\rm cm}^2\).

Statistics:

133 students sent a solution.
6 points:	86 students.
5 points:	12 students.
4 points:	10 students.
3 points:	3 students.
2 points:	5 students.
1 point:	3 students.
0 point:	13 students.
Unfair, not evaluated:	1 solutions.

Problems in Mathematics of KöMaL, December 2011