 Problem K. 316. (December 2011)
Problem K. 316. (December 2011)
K. 316. Find all common fractions that make a total of exactly 1 if added to 12/96, such that every digit occurs exactly once in the numerators and denominators of the two fractions together.
(6 pont)
Deadline expired on January 10, 2012.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. \(\displaystyle 12/96=1/8\), azaz a \(\displaystyle 7/8\) bővített alakját keressük. Legyen a keresett bővítés \(\displaystyle 7x/8x\). A bővített alak számlálója és nevezője összesen 6 számjegyet tartalmaz. Mivel a \(\displaystyle 7/8\) \(\displaystyle 1\)-nél kisebb, ezért a bővített tört kétjegyű/négyjegyű vagy háromjegyű/háromjegyű alakú lehet. Mivel a \(\displaystyle 99/1000\) a legnagyobb olyan szám, ami kétjegyű/négyjegyű alakú és \(\displaystyle 7/8 > 99/1000\), így a számlálóban és a nevezőben is háromjegyű számnak kell állnia. Ha \(\displaystyle 7x\) és \(\displaystyle 8x\) háromjegyű, akkor \(\displaystyle 14 < x < 125\). A számjegyek, amiket fel kell még használnunk: 0, 3, 4, 5, 7, 8. Ezért a számláló (ami kisebb, mint a nevező), nagyobb, mint 300, a nevező pedig kisebb, mint 900. Tehát (mivel a 38, 39, 40, 41 és 42 nem megoldások) \(\displaystyle 42 < x < 113\). Foglaljuk táblázatba \(\displaystyle x\), és ennek megfelelően \(\displaystyle 7x\) és \(\displaystyle 8x\) lehetséges utolsó számjegyeit.
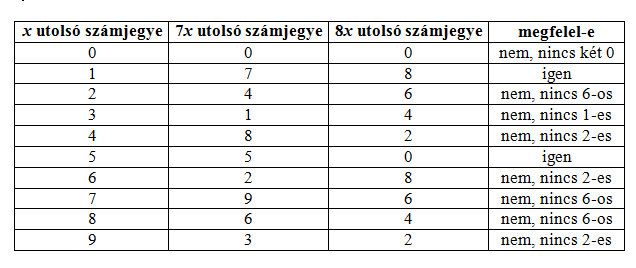
Így \(\displaystyle x\) értéke lehet: 45, 51, 55, 61, 65, 71, 75, 81, 85, 91, 95, 101, 105, 111. Ezeket kipróbálva összesen két megoldás adódik: \(\displaystyle (51\cdot7)/(51\cdot8) = 357/408\), és \(\displaystyle (105\cdot7)/(105\cdot8) = 735/840\).
Statistics:
173 students sent a solution. 6 points: Antal Zsófia, Bajnok Anna, Belényesi Máté, Csilling Tamás, Faragó Timea, Fekete Panna, Fülöp Erik, Gál István Marcell, Gnandt Balázs, Hartvig Áron, Hegyi Zoltán, Heszler András, Hódos Bálint, Holczer András, Jákli Aida Karolina, Jójárt Alexandra, Király 719 Ágnes, Koller Henrietta, Kovács 148 Dávid, Kovács 628 Márton, Maizl Noémi, Markó Gergely, Máthé Roland, Pál Balázs, Palkó Richárd, Pasztuhov Ágnes, Pátkai - Varga Ákos, Qian Lívia, Rátky Márton, Sziegl Benedek, Tamás Csongor, Tari Balázs, Tóth Ádám Bars, Tóth Adrián, Tóth László Gábor, Trinyik Flóra, Villám Kristóf, Virágh Anna. 5 points: Biczó Zsolt, Csiszár Tamás, Iványi Blanka, Mándoki Sára, Máté Bálint, Porupsánszki István, Sipos-Vajda Eszter, Somogyi Zoltán, Szeidl Balázs Vince, Vásárhelyi Bence. 4 points: 14 students. 3 points: 18 students. 2 points: 17 students. 1 point: 3 students. 0 point: 67 students. Unfair, not evaluated: 6 solutionss.
Problems in Mathematics of KöMaL, December 2011
