Problem K. 321. (January 2012)

K. 321. We cut a regular hexagon shaped tabletop into two parts along his symmetry diagonal, like this we got two symmetric trapezoid tabletops. In the reading area of a library, there are such trapezoidal tables in three colours: green, blue and red. We compiled a bigger regular hexagon from eight such tabletops.

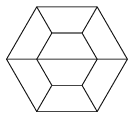
a) In how many different ways is it possible to make this arrangement if two tables of the same colour cannot have an edge in common? (Arrangements obtained from each other by rotation are not considered different.)

b) At the long side of a trapezoidal table there is room for two chairs, while at each of the other sides there is only room for one chair. Therefore, 12 people can be seated comfortably around this hexagonal arrangement of tables. How many tables are needed for a big hexagon around which 18 people can be comfortably seated?

(6 pont)

Deadline expired on February 10, 2012.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. a) A két középső asztal mindenképpen különböző színű. Legyen az ábrán a felső piros, az alsó kék. A legfelső asztal lehet kék vagy zöld. Ha kék, akkor az óramutató járása szerint körben haladva a szélső asztalok színe kék, zöld, piros, zöld, piros, zöld, ha pedig a legfelső szín zöld, akkor körben haladva az asztalok színe zöld, kék, a következő lehet piros vagy zöld, és így a befejezés kétféle: piros, zöld, piros, kék vagy pedig zöld, piros, zöld, kék. Tehát ebben az alapesetben háromféle megoldást találtunk. A középső két asztal színe háromféle lehet (a forgatás miatt csak az számít, hogy oda melyik két színt választottuk be), ezért a lehetőségek száma összesen 9.

b) Ha a trapéz rövidebbik oldalát egységnyinek tekintjük, akkor egy olyan hatszöget kell kiraknunk, melynek oldala nem két, hanem három egység hosszúságú. Ha elkezdjük kirakni, akkor könnyen látható, hogy egy ilyen hatszög létrehozásához 18 darab trapézra van szükségünk.

Statistics:

138 students sent a solution.
6 points:	Bajnok Anna, Belényesi Máté, Császma Péter, Csiki 778 Nikolett, Csilling Tamás, Dombrovszky Borbála, Farkas Margit, Fekete Panna, Geiszl András, Görgei Anna Mária, Hartvig Áron, Iványi Blanka, Jójárt Alexandra, Király 719 Ágnes, Kovács 113 András, Kurucz Réka, Lengyel Ádám, Maizl Noémi, Mándoki Sára, Markó Gergely, Máthé Roland, Nagy 288 Bence, Nagy Ágnes Judit, Qian Lívia, Rátky Márton, Ruzsbánszki Nándor, Sipos-Vajda Eszter, Somogyi Zoltán, Szegedi Bálint, Szép Márton István, Szigeti Gréta Anna, Tamás Csongor, Tatár Krisztina, Tim Márton, Tóth Adrián, Tóth László Gábor, Virágh Anna, Weisz Szilvia.
4 points:	11 students.
3 points:	3 students.
2 points:	45 students.
1 point:	3 students.
0 point:	31 students.
Unfair, not evaluated:	7 solutionss.

Problems in Mathematics of KöMaL, January 2012