Problem K. 330. (February 2012)

K. 330. A regular triangle ABF is inscribed in a square ABCD as shown in the figure. The length of AE is 2. What is the area of the square ABCD?

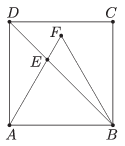
(6 pont)

Deadline expired on March 12, 2012.

Sorry, the solution is available only in Hungarian. Google translation

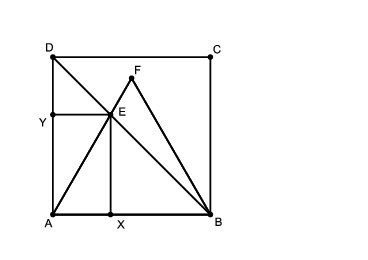
Megoldás. Rajzoljuk be az ábrába azt a téglalapot, melynek átlója \(\displaystyle AE\), oldalai pedig a négyzet oldalaival párhuzamosak: \(\displaystyle AXEY\), ahol \(\displaystyle X\) a négyzet \(\displaystyle AB\) oldalán van. Ekkor egyrészt az \(\displaystyle EXB\) egy egyenlő szárú, derékszögű háromszög, így \(\displaystyle EX=XB\). Másrészt az \(\displaystyle AXE\) háromszög "félszabályos", azaz egy szabályos háromszög fele, így oldalainak hossza \(\displaystyle AE=2\), \(\displaystyle AX=1\) és \(\displaystyle XE= \sqrt 3\). Ennek megfelelően a négyzet oldalának hossza \(\displaystyle AB=AX+XB=1+\sqrt 3\), azaz a területe \(\displaystyle (1+\sqrt 3)^2=4+2\sqrt 3\approx 7,46\).

Statistics:

139 students sent a solution.
6 points:	54 students.
5 points:	31 students.
4 points:	28 students.
3 points:	8 students.
2 points:	7 students.
1 point:	5 students.
0 point:	3 students.
Unfair, not evaluated:	3 solutionss.

Problems in Mathematics of KöMaL, February 2012