Problem K. 335. (March 2012)

K. 335. A peculiar calculator only has four buttons on it: 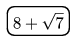(eight plus root seven), (addition), 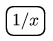(reciprocal) and (equals) (see the figure).

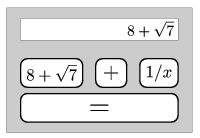
The calculator always carries out the operations with exact values, and it can also store the current value as a constant if the button is pressed twice. That is, in subsequent calculations whenever the button is pressed, the number is incremented by that value any number of times. (E.g. if the buttons 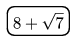        are pressed, it will display ). Prove that the result of the following sequence of operations is 1:

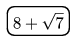
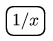
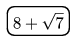
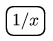
...  (56 times)

...  (15 times)

(6 pont)

Deadline expired on April 10, 2012.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A feladat példája szerint a \(\displaystyle 8+\sqrt 7\) reciprokát összeadtuk egymás után 57-szer \(\displaystyle \left( \frac{57}{8+\sqrt 7}\right)= \frac{57}{8+\sqrt 7}\cdot \frac{8-\sqrt 7}{8-\sqrt 7}=\frac{57(8-\sqrt 7)}{64-7}=8-\sqrt 7)\), majd ehhez hozzáadtuk a \(\displaystyle 8+\sqrt 7\)-et (a részeredmény: 16). Ennek reciprokát véve (1/16) a reciprokot egymás után 16-szor összedatuk. A végeredmény tehát \(\displaystyle 16\cdot \frac 1{16}=1\).

Statistics:

106 students sent a solution.
6 points:	54 students.
5 points:	9 students.
4 points:	29 students.
3 points:	12 students.
2 points:	1 student.
Unfair, not evaluated:	1 solutions.

Problems in Mathematics of KöMaL, March 2012