 Problem K. 342. (September 2012)
Problem K. 342. (September 2012)
K. 342. Triangle ABC in the figure is equilateral, AP bisects the angle at A. Prove that AP=BP+PC.
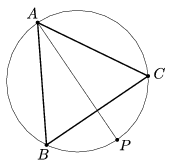
(6 pont)
Deadline expired on October 10, 2012.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Mivel a háromszög egyenlő szárú, ezért BP=PC. Így elég igazolni, hogy BP=AP/2. AP a kör átmérője, így Thalesz tétele miatt az ABP szög derékszög. Ekkor az ABP háromszög 60-30-90 fokos derékszögű háromszög, melyben BP a rövidebbik befogó, így egyenlő az átfogó felével. Ez éppen a bizonyítandó állítást jelenti.
Statistics:
214 students sent a solution. 6 points: 75 students. 5 points: 56 students. 4 points: 36 students. 3 points: 13 students. 2 points: 12 students. 1 point: 7 students. 0 point: 10 students. Unfair, not evaluated: 5 solutionss.
Problems in Mathematics of KöMaL, September 2012
