 Problem K. 360. (December 2012)
Problem K. 360. (December 2012)
K. 360. The accompanying figure is drawn on a square lattice. The separation of consecutive parallel grid lines is 5 mm. The polygon consists of 999 line segments. Determine its length, rounded to the nearest metre.
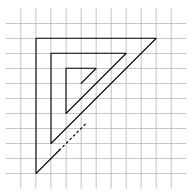
(6 pont)
Deadline expired on January 10, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Jelölje a rácsnégyzetek oldalának hosszát \(\displaystyle d\). Ekkor az átlójuk \(\displaystyle d\sqrt2\) hosszúságú. A kérdéses vonal \(\displaystyle S\) hossza:
\(\displaystyle S=d(1\cdot\sqrt2+2+3+4\cdot\sqrt2+5+6+7\cdot\sqrt2+...+997\cdot\sqrt2+998+999)=\)
\(\displaystyle =d\sqrt2(1+4+7+...+997)+d(5+11+17+...+1997).\)
Mindkét zárójelben 333 tagú összeg szerepel, ezeket össze tudjuk adni:
\(\displaystyle 1+4+7+...+997=\frac{998\cdot333}{2}=166167,\)
\(\displaystyle 5+11+17+...+1997=\frac{2002\cdot333}{2}=333333.\)
A kapott számokat és a \(\displaystyle d\) értékét centiméterben beírva:
\(\displaystyle S=0,5\cdot\sqrt2\cdot166167+0,5\cdot333333\approx284164~ (cm).\)
Vagyis a vonal hossza kb. 2842 méter.
Statistics:
127 students sent a solution. 6 points: Baglyas Márton, Bálint Roland Péter, Balog 6 Klaudia, Berekai Eszter, Bodonhelyi Anna, Borbás András, Bottlik Judit, Coulibaly Patrik, Csatári Jakab, Farkas Olivér, Garaba Flórián, Gulyás Gabriella, Herbály Blanka, Horváth 016 Gábor, Ipolyszegi Gábor, Ivankoviæ Mladen, Ivkovic Iván, Jób Csongor, Kálmán Fanni, Kaprinai Ádám, Kasza Bence, Keszthelyi Máté, Kis Levente, Kocsis Júlia, Kósa Szilárd, Kristóf Mátyás, Marticsek Réka, Matusek Lili, Matusek Márton, Mészáros 01 Viktória, Németh Flóra Boróka, Papp 535 Ágnes, Stefics Attila, Stumphauser Nóra, Surek Emese, Szabó 11 Dániel, Szabó Júlia, Szántó Kamilla, Szathmári Balázs, Szentgyörgyi Flóra, Szilágyi Botond, Szintai Kristóf, Szűcs Áron Ábrahám, Tóvári Gergő, Varga 123 Péter. 5 points: 35 students. 4 points: 17 students. 3 points: 9 students. 2 points: 5 students. 1 point: 6 students. 0 point: 8 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, December 2012
