 Problem K. 366. (January 2013)
Problem K. 366. (January 2013)
K. 366. What is the largest score that is impossible to achieve with the dart board shown, no matter how many darts are thrown?
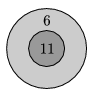
(6 pont)
Deadline expired on February 11, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A kidobható számokat így írhatjuk fel: \(\displaystyle a \cdot 6 + b \cdot 11\) (\(\displaystyle a\), \(\displaystyle b\) \(\displaystyle \in \Bbb N\)). Vizsgáljuk meg, hogy melyik az a legkisebb szám, amitől kezdve egyesével növelhető az összeg. Kétféleképpen lehet eggyel növelni az összeget: a) \(\displaystyle a + 2\) és \(\displaystyle b – 1\), \(\displaystyle a+13\) és \(\displaystyle b-7\) stb.; b) \(\displaystyle a – 9\) és \(\displaystyle b + 5\), \(\displaystyle a-20\) és \(\displaystyle b+11\) stb. Már csak megfelelő kezdőértékeket kell választani ahhoz, hogy valamelyik lépést mindig meg tudjuk tenni, méghozzá úgy, hogy az összeg a lehető legkisebb legyen. Ha egy b) lépéssel akarunk indítani, ahhoz \(\displaystyle a \geq 9\) kellene, azaz az összeg legalább 54 (utána már menne, hiszen ha \(\displaystyle b = 5\) az első lépés után, akkor amíg ezt ötször csökkentjük eggyel, \(\displaystyle a = 10\) lesz, amit újra lehet 9-cel csökkenteni, stb.). Ha a) lépéssel indítunk, akkor \(\displaystyle a = 0\) esetén ötször, \(\displaystyle a = 1\) esetén négyszer kell ezt a lépést ismételni, hogy egy b) lépés jöhessen. Ezt követően már folytatható újra a) lépéssel a növelés, hiszen \(\displaystyle b\) újra 5, és így tovább. A két eset közül az \(\displaystyle a = 1\), \(\displaystyle b = 4\) a kisebb, ekkor az összeg 50. Tehát a legnagyobb szám, amit nem lehet kidobni a 49.
Statistics:
96 students sent a solution. 6 points: Bodonhelyi Anna, Borbás András, Bottlik Judit, Coulibaly Patrik, Csatári Jakab, Cserna Koppány Levente, Domokos Vanessza, Fórián Levente, Galbács Márton, Györffy Orsolya, Herbály Blanka, Ipolyszegi Gábor, Kálmán Gergely, Kasó Ferenc, Kasó Gergő, Kasza Bence, Kis Levente, Kocsis Júlia, Kristóf Mátyás, László Márton, Mári László Levente, Matusek Márton, Mátyus Adrienn, Németh Flóra Boróka, Pálfi Mária, Papp 535 Ágnes, Papvári Dániel, Petrás Tamás, Pintér Gergő, Ratkovics Gábor, Sebastian Fodor, Stumphauser Nóra, Szabó 11 Dániel, Szalai Tibor Viktor, Szántó Benedek, Szathmári Balázs, Szűcs Áron Ábrahám, Szűcs Kilián Ádám, Varga 123 Péter, Varga Liza, Varga Stefánia. 5 points: 11 students. 4 points: 7 students. 3 points: 4 students. 2 points: 7 students. 1 point: 4 students. 0 point: 22 students.
Problems in Mathematics of KöMaL, January 2013
