 Problem K. 372. (February 2013)
Problem K. 372. (February 2013)
K. 372. With lines parallel to the diagonals, a cross is drawn in a square of side 10 cm, as shown in the diagram. The lines forming the boundary of the cross inside the square intersect the sides at equal distances from the vertices. What is the distance between the parallel lines forming a particular branch of the cross if the area of the cross is 64 cm2?
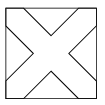
(6 pont)
Deadline expired on March 11, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A négyzet területe 100 \(\displaystyle \rm{cm}^2\). A négyzetnek a kereszten kívüli része négy darab derékszögű háromszög, melyek (elforgatás nélkül) egy négyzetté tolhatók össze. Ennek területe 100 – 64 = 36 \(\displaystyle \rm{cm}^2\), így oldalának hossza 6 cm. A nagy négyzet oldalából 4 cm marad a csúcsoktól vett távolságokra, tehát a kereszt szárát alkotó párhuzamosok a csúcsoktól 2 cm-re érnek ki a négyzet oldalaira. A keresett távolság így egy 2 cm befogójú, egyenlő szárú derékszögű háromszög átfogója, azaz \(\displaystyle 2\sqrt2\) cm.
Statistics:
128 students sent a solution. 6 points: 93 students. 5 points: 13 students. 4 points: 3 students. 3 points: 3 students. 2 points: 4 students. 1 point: 3 students. 0 point: 3 students. Unfair, not evaluated: 6 solutionss.
Problems in Mathematics of KöMaL, February 2013
