 Problem K. 383. (September 2013)
Problem K. 383. (September 2013)
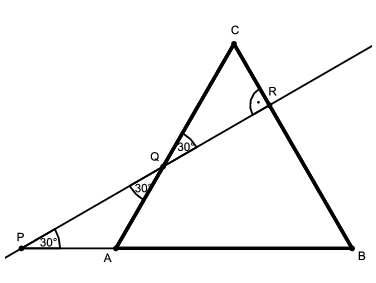
K. 383. Base AB of the regular triangle ABC is extended beyond vertex A by two fifths of the length AB, to get point P. Point P is connected to the point Q that lies on side AC (closer to A) and divides it 2:3. The resulting line intersects line CB at point R. Given that AP=2684, find the length of CR.
(6 pont)
Deadline expired on October 10, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. \(\displaystyle PA=QA=\frac25\cdot AB=2684\), amiből egyrészt \(\displaystyle AB=6710\), másrészt \(\displaystyle APQ\angle=AQP\angle=\frac{180^{\circ}-60^{\circ}}{2}=30^{\circ}\) következik. Mivel \(\displaystyle RQC\angle=AQP\angle=30^{\circ}\) és \(\displaystyle QCR\angle=ACB\angle=60^{\circ}\), ezért \(\displaystyle CRQ\angle=180^{\circ}-(RQC\angle+QCR\angle)=90^{\circ}\) és a \(\displaystyle CRQ\) háromszög egy szabályos háromszög fele. Ebből következik, hogy \(\displaystyle CR=QC/2=(AC-AQ)/2=(6710-2684)/2=4026/2=2013\).
Statistics:
241 students sent a solution. 6 points: 153 students. 5 points: 34 students. 4 points: 22 students. 3 points: 6 students. 2 points: 5 students. 1 point: 10 students. 0 point: 9 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, September 2013
