 Problem K. 384. (September 2013)
Problem K. 384. (September 2013)
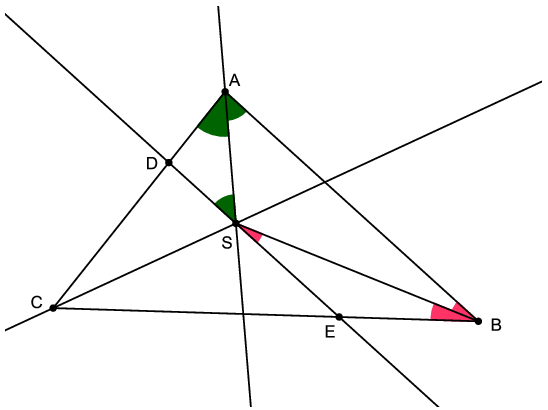
K. 384. Triangle ABC has an obtuse angle at vertex A. Denote the centre of the inscribed circle by S. The line drawn through S parallel to AB intersects side AC at D and side BC at E. Prove that DE=AD+BE.
German competition problem
(6 pont)
Deadline expired on October 10, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. \(\displaystyle BAS\angle=DSA\angle\), mert váltószögek. \(\displaystyle DAS\angle=BAS\angle\), mert \(\displaystyle AS\) szögfelező. Így \(\displaystyle DSA\angle=DAS\angle\), vagyis az \(\displaystyle ADS\) háromszög egyenlő szárú. Így \(\displaystyle AD=DS\).
Hasonlóan lehet belátni, hogy \(\displaystyle BE=SE\). Így pedig \(\displaystyle DE=DS+SE=AD+BE\).
Statistics:
202 students sent a solution. 6 points: 160 students. 5 points: 18 students. 4 points: 4 students. 3 points: 8 students. 2 points: 1 student. 0 point: 9 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, September 2013
