Problem K. 385. (October 2013)

K. 385. A square sheet of paper is folded, and then a piece of the folded sheet is cut off along a straight line. When the sheet is unfolded, a square hole is found at the centre, as shown in the figure. (The centres of the two squares coincide, and the sides of the small square are parallel to the diagonals of the large square.)

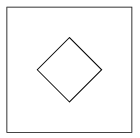
Find a possible combination of folding and cutting that produces the results described. Find a possible combination of folding and cutting in which the part removed is a rectangle, but not a square. (The sheet is folded and a piece is cut off along a straight line. The centres of the square and rectangle should coincide, and the sides of the rectangle are parallel to the diagonals of the square.)

(6 pont)

Deadline expired on November 11, 2013.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Sok megoldás van. Érdemes visszafelé gondolkodni: kivágunk egy négyzetet (téglalapot), majd úgy hajtjuk össze a nagy négyzetet, hogy a kis négyzet (téglalap) oldalai egymásra kerüljenek.

Egy lehetséges megoldás Abonyi-Tóth Barbaráé (Budapest, ELTE Apáczai Csere János gyak. Gimn.):

Először az egyik átlója mentén félbehajtjuk:

és azt a két csúcsot, amelyeket ez az átló összeköt, az eredeti négyzet oldalára merőlegesen behajtjuk úgy, hogy mind a négy csúcs egy helyre kerüljön.

Ezután már csak a keletkezett négyzet felső sarkát (az eredeti négyzet közepét) az oldalakkal 45°-os szöget bezárva kell levágnunk.

Az előzőhez hasonlóan itt is először félbehajtjuk a lapot az átlója mentén, de mivel téglalapot akarunk belőle kivágni és nem négyzetet, ezért az egyik oldalát meg kell nyújtanunk az eredeti négyzet átlójával párhuzamosan,

ezért az átló által összekötött két csúcsot nem hajtjuk le egészen addig, hogy a négy csúcs összeérjen, hanem a hajtásvonal közelebb van az átló által összekötött csúcsokhoz, mint a másik kettőhöz.

Utolsó lépésként a keletkezett ötszög felső oldalát kell levágnunk a többi oldallal \(\displaystyle 45^{\circ}\)-os szöget bezárva.

Statistics:

235 students sent a solution.
6 points:	111 students.
5 points:	29 students.
4 points:	38 students.
3 points:	33 students.
2 points:	18 students.
1 point:	2 students.
0 point:	1 student.
Unfair, not evaluated:	3 solutionss.

Problems in Mathematics of KöMaL, October 2013