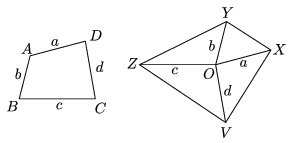
K. 39. The perimeter of a convex quadrilateral ABCD is cut at each vertex, and the four sides are parallel shifted to a common point O as shown in the Figure The endpoints of the line segments different from O are connected to form the quadrilateral XYZV. By what factor is the area of the quadrilateral XYZV greater than that of the original quadrilateral ABCD?

(6 points)

Deadline expired.

Sorry, the solution is published in Hungarian only.

Megoldás. Nézzük azokat az oldalpárokat, amelyek mindkét elrendezésben rendelkeznek közös csúccsal, pl. a BC, CD és az YO, ZO párokat. Mivel ezek páronként párhuzamosak, a BCD és a ZYO háromszögek területe megegyezik, ugyanis pl. a c-vel jelölt oldalhoz tartozó magasság mindkettőben ugyanakkora. Ugyanígy az ADC és a VOZ háromszögek, a BAD és az XOV háromszögek, valamint az ABC és XOY háromszögek is azonos területűek. Az ABCD négyszög területét azonban az említett négy háromszög kétszer teszi ki, míg az XYZV négyszögét egyszer, ezért az utóbbi területe kétszerese az előbbiének.

Statistics on problem K. 39. 85 students sent a solution. 6 points: C. Szabó Bence, Gecse 666 Gergely, Győri Tamás Noé, Horváth Markó, Kapás Gábor, Károly Dóra, Kiss 103 Dániel , Marincsák Miklós, Matyuska Péter, Mihálykó Ágnes, Nagy 777 Mariann, Poócza Katalin, Szécsényi Ágnes, Szeles Annamária, Talabér Dóra, Tallián György, Tokai-Kiss Ákos, Tolner Ferenc. 5 points: Balázs Attila, Gyurcsik Judit, Hoffmann Jenő, Kovács Blanka, Laki Balázs, Plesz Mónika, Sárvári Gábor. 4 points: 11 students. 3 points: 21 students. 2 points: 10 students. 0 point: 18 students.