 Problem K. 419. (March 2014)
Problem K. 419. (March 2014)
K. 419. Six congruent circles are drawn in a circular ring such that each of them touches the circles bounding the ring, and also touches the two adjacent circles. What percentage of the area of the ring is covered by the circles?
(6 pont)
Deadline expired on April 10, 2014.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A hat külső kör középpontja szabályos hatszöget alkot. Legyenek \(\displaystyle P\), \(\displaystyle R\) és \(\displaystyle S\) a kis körök érintési pontjai az ábra szerint. Mivel \(\displaystyle O_1OO_2\angle=60^{\circ}\), és \(\displaystyle OO_1=OO_2\), ezért az \(\displaystyle O_1OO_2\) háromszög szabályos. Így \(\displaystyle O_1O=O_1O_2\), azaz \(\displaystyle O_1P+PO=O_1R+RO_2\). Mivel \(\displaystyle O_1P=O_1R\), ebből \(\displaystyle PO=RO_2\) következik, tehát a belső kis kör sugara megegyezik a hat másik kör sugarával. Jelölje ezt a sugarat \(\displaystyle r\), a nagy kör sugarát pedig \(\displaystyle R\). Ekkor \(\displaystyle R=OT=OP+PO_1+O_1T=3r\).
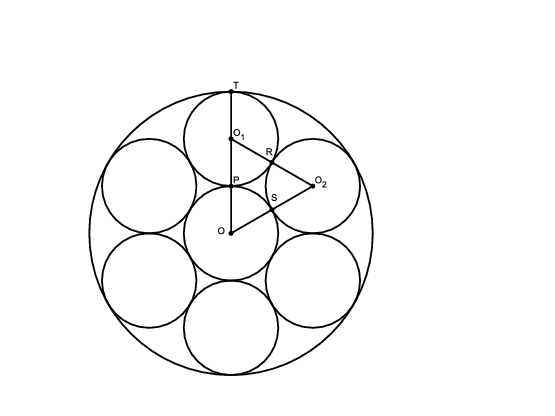
A körgyűrű területét megkapjuk, ha a nagy kör területéből kivonjuk a belső kis kör területét: \(\displaystyle t_{\rm kgy}=(3r)^2\pi-r^2\pi=8r^2\pi\).
A hat kör területének összege pedig \(\displaystyle t_6=6r^2\pi\).
A kettő aránya: \(\displaystyle \frac{6r^2\pi}{8r^2\pi}=\frac34\).
Statistics:
113 students sent a solution. 6 points: 69 students. 5 points: 12 students. 4 points: 14 students. 3 points: 9 students. 2 points: 2 students. 1 point: 3 students. 0 point: 2 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, March 2014
