Problem K. 422. (September 2014)

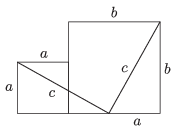
K. 422. Two squares of sides \(\displaystyle a\) and \(\displaystyle b\) are placed next to each other and then cut into five plane figures altogether with two line segments of length \(\displaystyle c\), as shown in the figure. Show that it is possible to build, without gaps or overlaps, a square of side \(\displaystyle c\) out of the five pieces.

(6 pont)

Deadline expired on October 10, 2014.

Statistics:

130 students sent a solution.
6 points:	Fekete Balázs Attila, Kós Anna, Kubovics Márton, Perényi Gellért, Sántha 001 Balázs, Sisák László Sándor, Szarka Álmos, Szilágyi Botond, Valkó Bence.
5 points:	Bácskai Zsombor, Cu Le Dieu Huong, Encz Koppány, Harsányi Benedek, János Zsuzsa Anna, Sepp Márton.
4 points:	18 students.
3 points:	17 students.
2 points:	16 students.
1 point:	46 students.
0 point:	14 students.
Unfair, not evaluated:	4 solutionss.

Problems in Mathematics of KöMaL, September 2014