Problem K. 489. (January 2016)

K. 489. Peter entered the first 2015 positive integers in a \(\displaystyle 100\times 100\) table, as shown in the figure. (In the figure, the table is not filled in completely yet.) What is the last number in the second row?

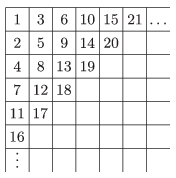
(6 pont)

Deadline expired on February 10, 2016.

Statistics:

102 students sent a solution.
6 points:	Bartha Ákos, Bertók Zsanett, Csóka Zoárd, Dékány Barnabás, Dobák Dániel, Fabó Bence Richárd, Fekete Barnabás, Gálffy Veronika, Gilicze Márton, Hoffmann Balázs, Jankovits András, Kávási Tamás, Keltai Dóra, Kertész Ferenc, Kluèka Vivien, Kovács 161 Márton Soma, Kovács 576 Kristóf, Marshall Tamás, Marton Laura, Mester Gyöngyvér, Mészáros 916 Márton, Miskolczi Abigél, Mónos Péter, Nagy Csaba Jenő, Nemes Balázs Boldizsár, Nyitrai Boglárka, Pálvölgyi Szilveszter, Pinke Jakab Zoltán, Pipis Panna, Polonyi Domonkos, Ruzsa Kata, Sal Dávid, Szöllősi Brigitta, Varga 294 Ákos, Zsótér Laura.
5 points:	Bálint Szilárd, Csáfordi József, Kiss 468 Péter, Nagy Gábor János, Piller Ádám.
4 points:	8 students.
3 points:	10 students.
2 points:	12 students.
1 point:	10 students.
0 point:	12 students.
Unfair, not evaluated:	10 solutionss.

Problems in Mathematics of KöMaL, January 2016