Problem K. 50.

Order KöMaL!

ELTE

Competitions Portal

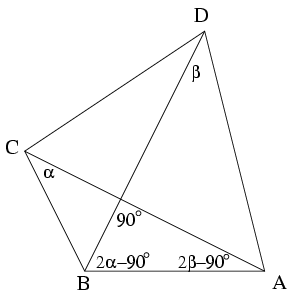
K. 50. In the quadrilateral ABCD, AB=AC=DB, and the diagonals are perpendicular. Find the sum of the angles ACB and ADB.

(6 points)

Deadline expired.

Sorry, the solution is published in Hungarian only.

Megoldás: Jelölje az ACB szöget $\alpha$ , az ADB szöget $\beta$ , az átlók metszéspontját E. Az ECB derékszögű háromszögben EBC $\angle$ =90^o- $\alpha$ , az EDA derékszögű háromszögben EAD $\angle$ =90^o- $\beta$ . Az ACB egyenlő szárú háromszög, tehát ABC $\angle$ = $\alpha$ , így ABE $\angle$ = $\alpha$ -(90^o- $\alpha$ )=2 $\alpha$ -90^o. Hasonlóan kapjuk az ABD egyenlő szárú háromszög felhasználásával, hogy BAE $\angle$ = $\beta$ -(90^o- $\beta$ )=2 $\beta$ -90^o. Az ABE derékszögű háromszöget tekintve 2 $\beta$ -90^o+2 $\alpha$ -90^o=90^o, innen $\alpha$ + $\beta$ =135^o.

Statistics on problem K. 50.

228 students sent a solution.

6 points: Balázsfalvi Balázs, Bedő Renáta, Bereczki 118 Katalin, Besnyő Réka, Bihari Mónika, Császár Orsolya, Csintalan Georgina, Egyed Zsombor, Erdész Zsombor Bálint, Glasenhardt Katalin, Gudenus Gergő, Heltai Botond, Herbály Gábor, Hoór Dorottya, Iván Dávid, Jónás Eszter, Kálló Gábor, Kazinczy Ádám, Király Csilla, Kovács Györgyi, Kovács Sarolta, Lang Péter, Lantos Tamás, Lovász Beáta, Márki Róbert, Meszlényi Regina, Michael Swift, Miklós Zita, Nagy Kitti, Németh 016 Mihály, Németh-Csóka Mihály, Orosz Ákos, Petrik Laura, Petróczy Dóra Gréta, Pótó Laura, Pupli Dorottya, Püsök László, Ravasz Dóra, Simon Attila, Sipos 234 Beáta, Stallenberger Alexa, Stumphauser 132 Tímea, Szabó 313 Gábor, Szabó 963 Noémi, Szabó Eszter, Szepesvári Dávid, Trásy Tamás, Werner Bence.

5 points: 50 students.

4 points: 30 students.

3 points: 9 students.

2 points: 6 students.

1 point: 33 students.

0 point: 41 students.

Unfair, not evaluated: 11 solutions.

Problems in Mathematics of KöMaL, October 2005

Our web pages are supported by:

ELTE