 Problem K. 507. (September 2016)
Problem K. 507. (September 2016)
K. 507. A six-pointed star is inscribed in each of two congruent regular hexagons. A smaller six-pointed star is then inscribed in the smaller hexagon formed inside the first star. The points of the star are the vertices of the corresponding hexagon in one case, and the midpoints of the sides of the hexagon in the other case. The resulting figures are shown in the diagram.
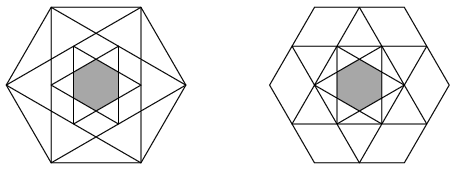
Compare the areas of the two small shaded hexagons.
(6 pont)
Deadline expired on October 10, 2016.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Kétféleképpen írtunk szabályos hatszögbe csillagot. Mindkét csillag két szabályos háromszög ugyanolyan módon való egymásra helyezése, tehát hasonlóak. Az első módszerben a csillagot tartalmazó hatszög és a csillag csúcsai megegyeznek. Tekintsük a csillagba írt szabályos hatszöget. Legyen ekkor \(\displaystyle b\) a kisebb és a nagyobb hatszög területének aránya, vagyis \(\displaystyle t_{nagy~hatszög}\cdot b=t_{kis~hatszög}\). A második módszerben a csillag csúcsai a csillagot tartalmazó hatszög oldalfelező pontjai. Tekintsük ekkor is a csillagba írt szabályos hatszöget, jelölje ekkor \(\displaystyle c\) az előbbi arányt.
A bal oldali ábrán előbb az első módszert használjuk, majd a belső hatszögbe írunk egy kisebb csillagot a második módszer szerint, így a besatírozott hatszög területe \(\displaystyle t_{nagy~hatszög}\cdot b\cdot c\). A jobb oldali ábrán pedig először a második, majd a keletkező hatszögbe az első módszer szerint írtunk csillagot, ezért a satírozott hatszög területe \(\displaystyle t_{nagy~hatszög}\cdot c\cdot b\). Tehát a két hatszög területe egyenlő.
Statistics:
100 students sent a solution. 6 points: 59 students. 5 points: 3 students. 4 points: 2 students. 3 points: 10 students. 2 points: 6 students. 1 point: 5 students. 0 point: 2 students. Unfair, not evaluated: 13 solutionss.
Problems in Mathematics of KöMaL, September 2016
