 Problem K. 508. (September 2016)
Problem K. 508. (September 2016)
K. 508. Earthquakes are getting more and more frequent in Wonderland. Several houses have developed cracks in the walls, some even fell down. The council of elders decided to reform building regulations. They became convinced that the condition for a brick wall being earthquake-proof is that no vertical or horizontal line should extend through it completely along the sides of the bricks. The dimensions of the bricks are \(\displaystyle 1 \times 2\).
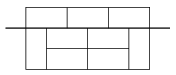
The wall in the figure is wrong, since there is a horizontal line cutting all through it
\(\displaystyle a)\) Design a plan for a \(\displaystyle 6 \times 8\) earthquake-proof wall, and another one for a \(\displaystyle 8 \times 8\) earthquake-proof wall.
\(\displaystyle b)\) Prove that it is impossible to build a \(\displaystyle 6 \times 6\) earthquake-proof wall.
(6 pont)
Deadline expired on October 10, 2016.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás.


A \(\displaystyle 6 \times 6\)-os fal \(\displaystyle 18\) téglából áll. A fal csak akkor lehet földrengésbiztos, ha minden vízszintes és függőleges, falon belül menő rácsvonal legalább egy téglát kettévág. És mivel a fal oldalhosszúságai párosak, ezért pl. egy oszlopban csak páros számú vízszintesen álló tégla lehet, tehát minden függőleges rácsvonal páros számú téglát vág ketté. Hasonló a helyzet a vízszintes rácsvonalakkal. Így a fal legalább \(\displaystyle (5 + 5) \cdot 2 = 20\) téglát vág ketté, ami ellentmondás, hiszen a fal 18 téglából áll. Tehát nincs \(\displaystyle 6\times6\)-os földrengésbiztos fal.

Statistics:
97 students sent a solution. 6 points: Bella Adrienn, Csikós Patrik, Czett Mátyás, Garami Júlia, Hervay Bence, Horváth 127 Ádám, Horváth 237 Lili, Juhász 315 Dorka, Kis 194 Károly, Kiss 7007 Bálint, Kozmér Barbara, Markó Gábor, Paróczai Anett, Sepsi Csombor Márton, Székelyhidi Klára, Szente Péter, Szirtes Botond, Vachal Krisztina, Vincze Lilla. 5 points: Bohus Ádám, Gyuricza Gergő, Lockár Miklós. 4 points: 5 students. 3 points: 5 students. 2 points: 50 students. 1 point: 10 students. 0 point: 4 students. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, September 2016
