Problem K. 518. (November 2016)

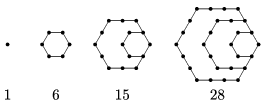
K. 518. The numbers in the figures and further figures created in the same way are called hexagonal numbers. Without proof, find a formula for the \(\displaystyle n\)th hexagonal number, and use it to show that 2016 is a hexagonal number.

(6 pont)

Deadline expired on December 12, 2016.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. „Emeletenként” nézve: \(\displaystyle 1 = 1 \cdot 1\), \(\displaystyle 6 = 3 \cdot 2\), \(\displaystyle 15 = 5 \cdot 3\), \(\displaystyle 28 = 7 \cdot 4\), az ötödik hatszögszám \(\displaystyle 9 \cdot 5 = 45\), a hatodik pedig \(\displaystyle 11 \cdot 6 = 66\) és így tovább. Az n. hatszögszám \(\displaystyle (2n – 1) \cdot n\). Mivel \(\displaystyle 2016 = 63 \cdot 32\), így a 2016 a 32. hatszögszám.

Statistics:

101 students sent a solution.
6 points:	84 students.
4 points:	6 students.
3 points:	2 students.
2 points:	5 students.
1 point:	1 student.
0 point:	3 students.

Problems in Mathematics of KöMaL, November 2016