K. 52. Egy város parkjában az ábrán látható sétaútrendszert akarják megépíteni. Összesen hány méter utat kell építeniük, ha az ábrán jelölt útszakaszok hossza 60, illetve 30 méter?

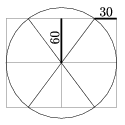
(6 pont)

A beküldési határidő LEJÁRT.

Megoldás: Legyen a kör sugara 30+x méter. Az x, 60, 30+x oldalú derékszögű háromszögre felírva a Pitagorasz-tételt: x²+60²=(x+30)², ebből x=45 méter. Az összes megépítendő út hossza tehát: 10^.75+6^.60+150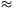^.1581,24 méter.

A K. 52. feladat statisztikája 210 dolgozat érkezett. 6 pontot kapott: 68 versenyző. 5 pontot kapott: 43 versenyző. 4 pontot kapott: 37 versenyző. 3 pontot kapott: 18 versenyző. 2 pontot kapott: 12 versenyző. 1 pontot kapott: 13 versenyző. 0 pontot kapott: 17 versenyző. Nem versenyszerű: 2 dolgozat.