Problem K. 523. (December 2016)

K. 523. Given a two-digit positive integer, we multiply its digits to get a new number. If the new number has two digits, then we multiply the digits again. This process is continued until a one-digit number is obtained. How many two-digit positive integers are there for which the process will terminate at the number 8?

(6 pont)

Deadline expired on January 10, 2017.

Sorry, the solution is available only in Hungarian. Google translation

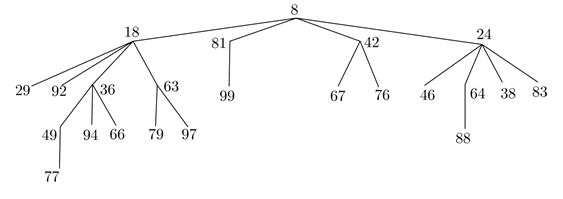
Megoldás. A 8-at 18-ból, 81-ből, 24-ből vagy a 42-ből kaphattuk.

A 18-at egyrészt 29-ből vagy 92-ből kaphattuk, melyek kiindulási számok lehettek csak, illetve 36-ból és 63-ból, melyeket 66-ból, 49-ből, 94-ből, illetve 79-ből és 97-ből kaphattunk.

A 66, 94, 79, 97 kiindulási számok lehettek csak, a 49-et kaphattuk a 77-ből.

81-et 99-ből kaphattunk. Ez már csak kiindulási szám lehetett.

24-et 46-ból, 64-ből, 38-ból, 83-ból kaphattunk. A 46, 38 és 83 csak kiindulási számok lehettek.

64-et 88-ból kaphattunk, amely csak kiindulási szám lehet.

42-t 67-ből vagy 76-ból, melyek csak kiindulási számok lehettek.

A megfelelő kétjegyű számok: 18, 81, 42, 24, 29, 92, 36, 63, 99, 67, 76, 46, 64, 38, 83, 49, 94, 66, 79, 97, 88, 77.

Tehát 22 ilyen kétjegyű szám van.

Statistics:

129 students sent a solution.
6 points:	67 students.
5 points:	19 students.
4 points:	18 students.
3 points:	18 students.
2 points:	5 students.
1 point:	2 students.

Problems in Mathematics of KöMaL, December 2016