 Problem K. 526. (December 2016)
Problem K. 526. (December 2016)
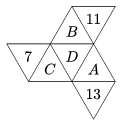
K. 526. In the diagram, each letter or number stands for a different prime number, and the sum of the four numbers in every ``straight line'' of triangles is the same. What is the smallest possible value of this sum?
(6 pont)
Deadline expired on January 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. \(\displaystyle B + D + A + 13 = A + D + C +7\), ahonnan \(\displaystyle B + 6 = C\).
\(\displaystyle A + D + C + 7 = C + D + B +11\), ahonnan \(\displaystyle A = B + 4\).
Vagyis \(\displaystyle C = A + 2\) és \(\displaystyle B\), \(\displaystyle B+4\), \(\displaystyle B+6\) egyaránt prímszámok.
A prímszámok: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, …
Mivel a 7, 11, 13 már szerepel a számok között, így a legkisebb lehetséges érték \(\displaystyle A = 41\), \(\displaystyle B = 37\), \(\displaystyle C = 43\), ekkor \(\displaystyle D = 2\). Az összeg legkisebb értéke 93.
(Ellenőrzés: \(\displaystyle 93 = 41 + 2 + 43 + 7 = 43 + 2 + 37 + 11 = 37 + 2 + 41 + 13)\).
Statistics:
99 students sent a solution. 6 points: 52 students. 5 points: 16 students. 4 points: 22 students. 3 points: 3 students. 2 points: 5 students. 0 point: 1 student.
Problems in Mathematics of KöMaL, December 2016
