 Problem K. 529. (January 2017)
Problem K. 529. (January 2017)
K. 529. Four circles are arranged as shown in the figure. The numbers \(\displaystyle 1, 2, 3, \ldots, 10\) are to be written in the ten regions formed by the circles such that the sum of the numbers within each circle is the same. What is the largest possible value of that sum?
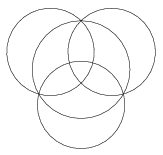
(6 pont)
Deadline expired on February 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Jelöljük az ábrán látható módon az egyes részekbe beírt számokat.
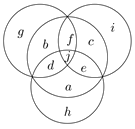
A feltételek miatt: \(\displaystyle a+e+c+f+b+d+j=g+f+b+d+j\), amiből \(\displaystyle a + e + c = g\). Hasonlóan: \(\displaystyle a + d + b = i\) és \(\displaystyle b + f + c = h\).
A belső körben akkor lesz a számok összege a legnagyobb, ha a \(\displaystyle g+h+i \) összeg a lehető legkisebb. Összeadva a három utóbbi egyenletet: \(\displaystyle 2(a + b + c) + (d +e +f) = g + h + i\). Ezek szerint \(\displaystyle g + h + i\) legkisebb értéke \(\displaystyle 2(1 + 2 + 3) + (4 + 5 + 6) = 27\). Ez csak úgy lehetséges, hogy \(\displaystyle g\), \(\displaystyle h\), \(\displaystyle i\) valamilyen sorrendben 8, 9, 10, az \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) számok pedig az 1, 2, 3 valamilyen sorrendben, illetve \(\displaystyle j = 7\).
A belső körben a számok összege ekkor \(\displaystyle 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28\).
Egy lehetséges megvalósítás:
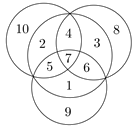
Ekkor mind a négy körben 28 az összeg, tehát valóban ez a lehetséges legnagyobb összeg.
Statistics:
65 students sent a solution. 6 points: Acs Imre, Csótai Enikő, Espán Márton, Gém Viktória, Görgei Botond Péter, Györfi Bence, Hegedűs Eszter, Horváth 237 Lili, Juhász 315 Dorka, Kis 194 Károly, Kozák 023 Áron, Kulisity Mátyás, Markó Gábor, Pásti Bence, Réz 426 Dávid, Sándor 111 Réka, Szabó 808 Álmos Levente, Szajkó Bence Gergő, Székelyhidi Klára. 5 points: Cseh Dániel, Jelinek Dorka, Kovács Fruzsina Dóra, Kreisz Bálint, Op Den Kelder Júlia, Rátki Luca, Rusvai Miklós, Szilágyi Anna Sára, Veres Kristóf, Vincze Lilla. 4 points: 11 students. 3 points: 7 students. 2 points: 3 students. 1 point: 3 students. 0 point: 1 student. Unfair, not evaluated: 11 solutionss.
Problems in Mathematics of KöMaL, January 2017
