 Problem K. 531. (January 2017)
Problem K. 531. (January 2017)
K. 531. Let us consider a \(\displaystyle 4\times 4\) chessboard. In each step, the colour of every square in a chosen \(\displaystyle 2\times 2\) block is changed (black to white, and white to black).
\(\displaystyle a)\) By performing some of these steps, is it possible to obtain a completely black board?
\(\displaystyle b)\) Is this possible in the case of a \(\displaystyle 5\times 5\) board, provided that the corners are initially white?
(6 pont)
Deadline expired on February 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. a) Igen, elérhető. Például a felső középső \(\displaystyle 2\times2\)-es és az alsó középső \(\displaystyle 2\times2\)-es változtatása után, majd egy-egy átellenes sarokban lévő \(\displaystyle 2\times2\)-es változtatása után már csak a középső sávot kell megváltoztatni.
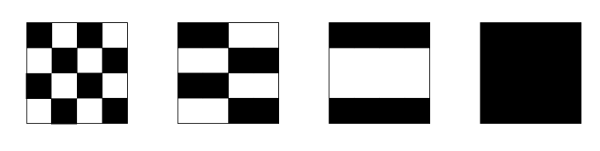
b) Egy-egy ilyen átszínezéskor a különböző színű mezők számának különbsége 4-gyel változik, vagy nem változik. (0-4-ből 4-0, 1-3-ból 3-1, 2-2-ből 2-2 lesz.) Kezdetben a fehér és a fekete mezők számának különbsége 1, az elérendő végállapotban pedig \(\displaystyle –25\). Az 1 és a \(\displaystyle –25\) különbsége 26, ami 4-gyel nem osztható, így nem lehetséges a kívánt átszínezés.
Statistics:
90 students sent a solution. 6 points: Bérczi Péter, Bohus Ádám, Cseh Dániel, Csikós Patrik, Espán Márton, Falvay Júlia, Görgei Botond Péter, Györfi Bence, Gyuricza Gergő, Hegedűs Eszter, Juhász 315 Dorka, Kereszes Kornél 537, Kincses Benedek, Kis 194 Károly, Kocsor Dániel, Kovács Fruzsina Dóra, Kozák 023 Áron, Kozák 023 Balázs, Markó Gábor, Mátravölgyi Bence, Mendei Barna, Német Franciska, Paróczai Anett, Rosztoczy Csaba, Szajkó Bence Gergő, Szemerédi Előd, Tornyi Napsugár, Veres Kristóf, Vincze Lilla. 5 points: 32 students. 4 points: 9 students. 3 points: 4 students. 2 points: 7 students. 0 point: 1 student. Unfair, not evaluated: 8 solutionss.
Problems in Mathematics of KöMaL, January 2017
