 Problem K. 535. (February 2017)
Problem K. 535. (February 2017)
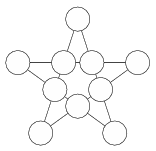
K. 535. Is it possible to arrange the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10 in the star pentagon in the figure, so that the sum of the numbers is the same along each line of four points?
(6 pont)
Deadline expired on March 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Minden szám pontosan két összegben szerepel. \(\displaystyle 2 \cdot (1 +2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10) = 110\), így minden egyenes mentén 110 : 5 = 22 kell legyen a számok összege.
Próbáljuk megkeresni, hogy az 1-est tartalmazó két egyenesen mely számok szerepelhetnek még. Hét számnégyes alkotható az 1-10-ig terjedő számokból úgy, hogy a bennük szereplő négy szám összege 22 legyen, és az 1-est tartalmazzák: 1,2 9,10; 1,3,8,10; 1,4,7,10; 1,4,8,9; 1,5,6,10; 1,5,7,9; 1,6,7,8. Annak a két egyenesnek, amelyeknek az 1-es közös eleme, más közös eleme nem lehet. Így a fenti számnégyesekből három olyan pár alkotható, melyek az 1-est tartalmazó két egyenesen szereplő számok lehetnek:
| egyik egyenesen szereplő számok | másik egyenesen szereplő számok | a hiányzó számok, melyek másol állnak | |
| I. eset | 1,2,9,10 | 1,6,7,8 | 3,4,5 |
| II. eset | 1,3,8,10 | 1,5,7,9 | 2,4,6 |
| III. eset | 1,4,8,9 | 1,5,6,10 | 2,3,7 |
I. eset. A 2, 9 és a 10-es számhoz is kell egy-egy számot választani a 6,7 és 8 közül úgy, hogy a 3,4,5 közül valamelyik kettővel az összeg 22 legyen. Nézzük először a 10-et. 22-10-6=6, de 3+4=7 már több a 6-nál. Ha nem a 6-ot, hanem a 7-et vagy a 8-at választjuk, akkor is nagyobb lesz a 7 a szükséges számnál.
II. eset. Az első esethez hasonlóan a 10-et nézzük, hozzá kell az 5, 7 és 9 számok közül választani egyet úgy, hogy a 2,4,6 közül valamelyik kettővel az összeg 22 legyen. Mivel 22-10-5=7, de a 2,4,6-ból képezhető összegek mind párosak, ez nem lehetséges. Az 5 helyett a 7 és a 9 választása esetén is ugyanez a helyzet.
III. eset. Itt a második oszlopban szerepel a 10, amihez a 4,8,vagy 9 közül egyet, illetve a 2,3,7 közül kell kettőt kiválasztani. Ez utóbbi esetén a lehetséges összegek: 2+3=5, 2+7=9 és 3+7=10. Mivel 22-10-4=8, 22-10-8=4 és 22-10-9=3, ezért itt sem jutunk célhoz.
Tehát nem lehet így elrendezni a számokat.
Csikós Patrik (Budapest, XIV. Kerületi Szent István Gimnázium) megoldása alapján
Statistics:
53 students sent a solution. 6 points: Acs Imre, Bérczi Péter, Gém Viktória, Juhász 315 Dorka, Kis 194 Károly, Kovács Fruzsina Dóra, Markó Gábor, Rátki Luca, Rusvai Miklós, Székelyhidi Klára, Szemerédi Előd, Vincze Lilla. 5 points: Csikós Patrik, Sándor 111 Réka. 4 points: 1 student. 3 points: 1 student. 2 points: 22 students. 1 point: 14 students. 0 point: 1 student.
Problems in Mathematics of KöMaL, February 2017
