 Problem K. 536. (February 2017)
Problem K. 536. (February 2017)
K. 536. For the angles of the star pentagon in the figure, determine the value of \(\displaystyle \alpha + \beta + \gamma +\delta + \varepsilon\).
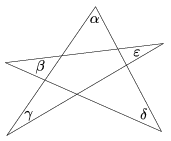
(6 pont)
Deadline expired on March 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A belső ötszög külső szögeinek kétszeres összegét kell levonni az öt kisháromszög belső szögeinek összegéből: \(\displaystyle 5\cdot 180^{\circ} – 2 \cdot 360^{\circ} = 180^{\circ}\).
Másképp (vázlat). Forgassunk körbe egy egyenest alfából indulva mindig a csúcsok körül (betűzzük meg a csúcsokat), először alfa, aztán delta, aztán béta, aztán epszilon, aztán gamma szöggel forgatunk, és pont 180 fokkal forgattuk körbe az egyenest.
Statistics:
80 students sent a solution. 6 points: 78 students. 5 points: 1 student. 1 point: 1 student.
Problems in Mathematics of KöMaL, February 2017
