Problem K. 539. (February 2017)

K. 539. In how many different ways is it possible to write the numbers 1, 2, 3, 4, 5, 6, 7 and 8 on the vertices of a cube, so that the sum of the four numbers is the same around each face of the cube? (Two solutions are considered the same if each number has the same neighbours adjacent to it.)

(6 pont)

Deadline expired on March 10, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Tekintsünk egy lapot és az azzal szemközti lapot. A két lap csúcsaiban álló számok összege egyenlő, így ez az összeg az összes szám összegének a fele. Mivel \(\displaystyle 1+2+3+4+5+6+7+8=\frac{8\cdot9}{2}=36\), így egy lap négy csúcsában álló számok összege 18.

Ezt felhasználva azt kapjuk, hogy egy olyan lapon, melyen a 8-as szám szerepel, a másik három szám a következő lehet: 1, 2, 7; 1, 3, 6; 1, 4, 5; 2, 3, 5.

A 8-cal szomszédos csúcsokra csak olyan számok kerülhetnek, melyek legalább két felbontásban szerepelnek. Négy ilyen szám van: 1, 2, 3, 5. Az 1 három felbontásban szerepel. Mivel összesen négy felbontás van, így az 1-esnek két lapon is szerepelnie kell, tehát egy 8-cal szomszédos csúcson kell lennie. A 8 és a vele szomszédos három szám egyértelműen meghatározza a többi számot is. (Előbb a 8-cat tartalmazó három lapon a hiányzó számokat, végül a nyolcadik. csúcshoz tartozó számot.)

Három megoldás van:

1. megoldás: a 8-cal szomszédos három szám az 1, a 2 és a 3.

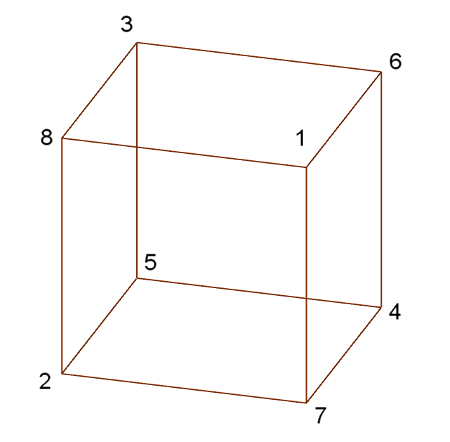
2. megoldás: a 8-cal szomszédos három szám az 1, a 2 és az 5.

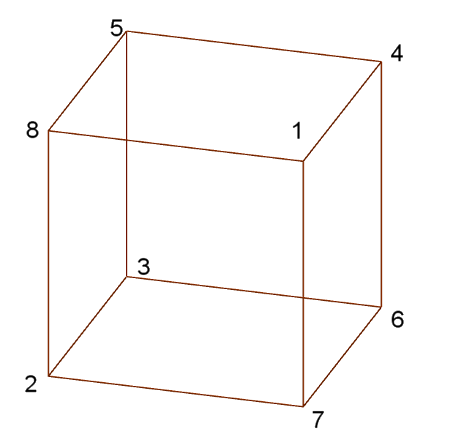
3. megoldás: a 8-cal szomszédos három szám az 1, a 3 és az 5.

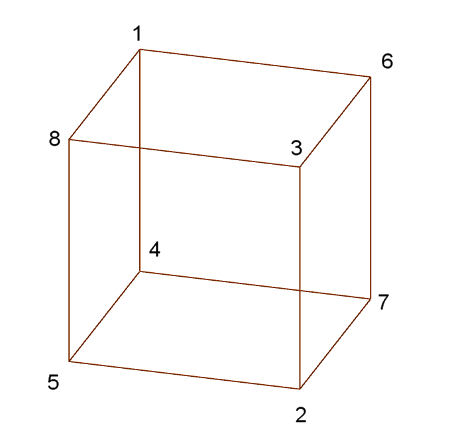
Kocsor Dániel (9. o. t, Szeged, SZTE Gyak. Gimn. és Ált. Isk.) megoldásának felhasználásával

Statistics:

55 students sent a solution.
6 points:	Acs Imre, Gém Viktória, Görgei Botond Péter, Juhász 315 Dorka, Kis 194 Károly, Kocsor Dániel, Markó Gábor, Mátravölgyi Bence, Mendei Barna, Szajkó Bence Gergő, Székelyhidi Klára, Szemerédi Előd.
5 points:	Balogh Bence, Bérczi Péter, Csikós Patrik, Espán Márton, Kovács Fruzsina Dóra, Merkl Levente.
4 points:	9 students.
3 points:	20 students.
2 points:	6 students.
0 point:	2 students.

Problems in Mathematics of KöMaL, February 2017