 Problem K. 544. (March 2017)
Problem K. 544. (March 2017)
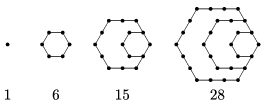
K. 544. Triangular numbers are defined as the numbers that can be represented as the sum of the first few consecutive natural numbers (\(\displaystyle 1, 3, 6, 10, \ldots\)). Hexagonal numbers are defined by the (infinite) sequence of diagrams represented below. Find all hexagonal numbers that are also triangular numbers.
(6 pont)
Deadline expired on April 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. ,,Emeletenként" nézve: \(\displaystyle 1 = 1 \cdot 1\), \(\displaystyle 6 = 2 \cdot 3\), \(\displaystyle 15 = 3 \cdot 5\), \(\displaystyle 28 = 4 \cdot 7\) és így tovább. Az \(\displaystyle n\). hatszögszám \(\displaystyle n(2n – 1)\). A \(\displaystyle k\). háromszögszám \(\displaystyle \frac{k(k+1)}{2}\).
Megoldandó a \(\displaystyle \frac{k(k+1)}{2}=n(2n-1)\) diofantikus egyenlet a pozitív számok halmazán. 2-vel beszorozva: \(\displaystyle k(k+1)=2n(2n-1)\), \(\displaystyle k^2+k=4n^2-2n\), átrendezve és szorzattá bontva: \(\displaystyle 2n+k=4n^2-k^2=(2n+k)(2n-k)\), ahonnan a pozitív \(\displaystyle (2n+k)\)-val elosztva: \(\displaystyle 1 = 2n – k\), vagyis \(\displaystyle k=2n-1\).
Tehát az \(\displaystyle n\)-dik hatszögszám éppen a \(\displaystyle (2n – 1)\)-dik háromszögszám, azaz minden hatszögszám háromszögszám is. (Illetve minden páratlanadik háromszögszám egyúttal hatszögszám is.)
Statistics:
54 students sent a solution. 6 points: Acs Imre, Balogh Bence, Bérczi Péter, Cseh Dániel, Espán Márton, Gém Viktória, Gyuricza Gergő, Hegedűs Eszter, Juhász 315 Dorka, Kincses Benedek, Kis 194 Károly, Kocsor Dániel, Kozák 023 Áron, Lakatos Zselyke, Lezsák Domonkos, Markó Gábor, Mátravölgyi Bence, Német Franciska, Op Den Kelder Júlia, Paróczai Anett, Pásti Bence, Purgel Dóra, Rátki Luca, Rittberger András, Rusvai Miklós, Sepsi Csombor Márton, Szente Péter, Vass Erik Márk, Vincze Lilla. 5 points: Csikós Patrik, Dombai Zétény, Fenyvesi Tamás, Nagy 345 Bálint, Pálfi Bálint, Szemerédi Előd. 4 points: 10 students. 3 points: 4 students. 2 points: 1 student. Unfair, not evaluated: 4 solutionss.
Problems in Mathematics of KöMaL, March 2017
