Problem K. 545. (March 2017)

K. 545. The three solids shown in the diagrams below are made up of small cubes. If the construction is continued in the same way, how many small cubes will the tenth solid consist of?

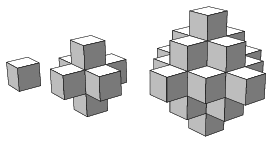
(6 pont)

Deadline expired on April 10, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Számoljunk rétegenként: a tizedik építményben 1-es, 2-es, 3-as, ..., 10-es rétegek vannak, bennük rendre 1, \(\displaystyle 4 + 1 = 5\) és \(\displaystyle 9 + 4 = 13\),..., \(\displaystyle 10^2 + 9^2\) kis kockával, ugyanis az egyes rétegekben sakktáblaszerű színezést alkalmazva kiderül, hogy az \(\displaystyle n\). szinten \(\displaystyle n^2+(n-1)^2\) darab kocka van.

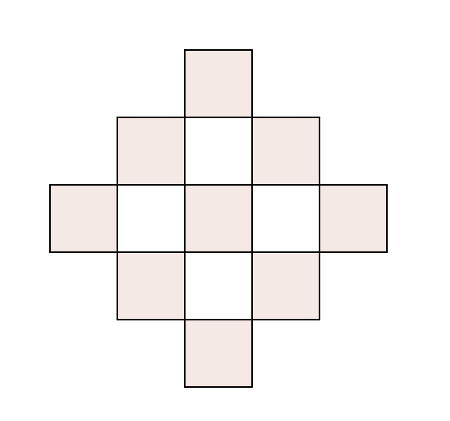
A tizedik testben összesen:

\(\displaystyle 1^2+(2^2+1^2)+(3^2+2^2)+...+(9^2+8^2)+(10^2+9^2)+(9^2+8^2)+...+(3^2+2^2)+(2^2+1^2)+1^2=\)

\(\displaystyle =4\cdot(1^2+2^2+3^2+\dots+8^2)+3\cdot9^2+10^2\)

kockából áll.

Ami számológéppel, vagy az első \(\displaystyle n\) pozitív négyzetszám összegére vonatkozó képlettel számolva:

\(\displaystyle 4\cdot\frac{8\cdot9\cdot17}{6}+3\cdot9^2+10^2=1159.\)

Tehát a 10. test 1159 kockából áll.

Statistics:

61 students sent a solution.
6 points:	51 students.
4 points:	2 students.
2 points:	3 students.
1 point:	3 students.
0 point:	2 students.

Problems in Mathematics of KöMaL, March 2017