Problem K. 60. (November 2005)

K. 60. The structure shown in the diagram was obtained by glueing identical cubes together. Two cubes may be glued together only if their joining faces overlap to some extent (that is, it is not enough if they meet in an edge). Find the minimum number of cubes needed to build the structure in the diagram.

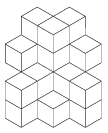
(6 pont)

Deadline expired on December 12, 2005.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás: Az ábrán láthatunk 13 kockát, és nyilván vannak nem látható kockák, melyek egyben tartják a többit.

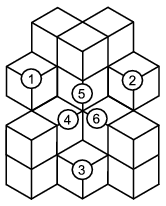
Az 1, 2, 3 jelű kockák rögzítéséhez darabonként egy nem látható kocka szükséges, ugyanis ezek távolsága akkora, hogy egy kocka nem tud közülük kettőhöz csatlakozni ragasztási felülettel. Össze kell még ragasztani a 4, 5 6 jelű kockákat is, ehhez kell egy kocka. Ez a kocka nem lehet az, amelyik pl. az 1-es kockát rögzíti, mert az 1, 4, 5 jelű kockáknak elhelyezkedésük miatt nem lehet egy (nem látható) kockával közös ragasztási felületük. Tehát legalább négy nem látható kocka szükséges a rögzítéshez. Ez elég is: a 4, 5, 6 jelű kockák a természetesen mögéjük kívánkozó, hozzájuk teljes oldallal csatlakozó kockával összeragaszthatók, az 1 és 2 jelű kockákat a hozzájuk, illetve az 5 jelű kockához teljes lappal csatlakozó egy-egy kockával rögzíthetjük, a 3 jelűt pedig hozzá és a 4-eshez vagy 6-oshoz teljes lappal csatlakozó kockával tudjuk felragasztani. Az építmény tehát legalább 17 kockából áll.

Statistics:

197 students sent a solution.
6 points:	109 students.
4 points:	7 students.
3 points:	3 students.
2 points:	22 students.
0 point:	53 students.
Unfair, not evaluated:	3 solutionss.

Problems in Mathematics of KöMaL, November 2005