Problem K. 61. (December 2005)

K. 61. There is a 20 by 10-metre rectangular park next to one of the chateaux on the Loire. A rectangular spiral path of 1 metre width leads to the interior of the park. The lord of the chateau walks down the spiral path every morning (always staying in the middle of the path and making right-angle turns at the corners), waters the white daisies he grows in a square flowerbed 1 m on a side, and then he walks back. What is the distance he covers altogether?

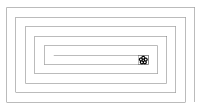
(6 pont)

Deadline expired on January 10, 2006.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás:

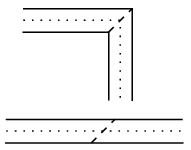
Ha a csigavonalban lévő utat az ábrának megfelelően daraboljuk át minden saroknál - a levágott darabot átfordítva illesztjük a másikhoz; pontozott vonal jelöli a kastély urának útvonalát -, akkor egy 1 méter széles, 200 m² területű, téglalap alakú útsávot kapunk, melynek hosszúsága (az utolsó 1 métert nem számítva) megegyezik a kastély ura által megtett út hosszával. Az útsáv területéből kiszámítható a hossza, amely 200 méter, az utolsó 1 métert nem számítva 199 méter. Ezt az úr mindennap kétszer teszi meg (oda és vissza), tehát az által megtett teljes út hossza 398 méter.

Statistics:

245 students sent a solution.
6 points:	163 students.
5 points:	39 students.
4 points:	35 students.
3 points:	6 students.
2 points:	1 student.
Unfair, not evaluated:	1 solutions.

Problems in Mathematics of KöMaL, December 2005