 Problem K. 62. (December 2005)
Problem K. 62. (December 2005)
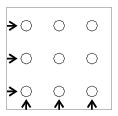
K. 62. Sophie has a toy that contains 9 wooden rods of different colours sticking out of a square wooden board, as shown in the figure. It is a logical puzzle. The task is to place nine red, nine green, and nine blue rings of the same shape on the rods. Each rod should have three rings of different colours on it, and at each level, the colours of the three rings along the directions indicated by the arrows in the diagram should also be different. In how many arrangements can the rings be placed on the rods? (Two arrangements count as different if there is at least one rod on which the order of the rings is different.)
(6 pont)
Deadline expired on January 10, 2006.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás:
A legalsó szinten a karikák elhelyezésére 12 lehetőségünk van:
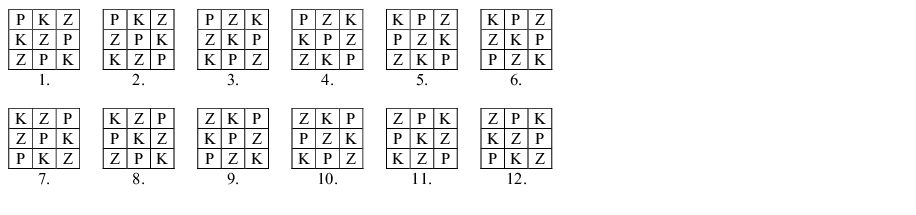
A középső szinten az alsó szint minden elrendezéséhez 2-féle elrendezést párosíthatunk (pl. az 1. számú elrendezéshez a 7. és 11. számút), a harmadik szintet pedig az első két szinten elhelyezett karikák színe meghatározza (a harmadik szinten minden oszlopra a rajta még nem szereplő színű karikát kell tenni). Így összesen 24 különböző helyes elrendezés található a karikákhoz.
Statistics:
132 students sent a solution. 6 points: 67 students. 5 points: 1 student. 4 points: 4 students. 3 points: 15 students. 2 points: 9 students. 1 point: 19 students. 0 point: 16 students. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, December 2005
