 Problem K. 63. (December 2005)
Problem K. 63. (December 2005)
K. 63. In the triangle ABC, X is the midpoint of side AB and Y is the midpoint of side AC. BY and CX intersect at S. Show that a) the areas of the triangles SBX and SCY are equal; b) the areas of triangle SBC and quadrilateral AXSY are equal.
(6 pont)
Deadline expired on January 10, 2006.
Sorry, the solution is available only in Hungarian. Google translation
Megoldások.
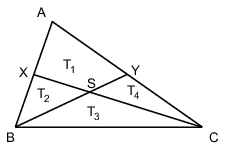
I. megoldás: a) XY a háromszög középvonala, mely párhuzamos BC-vel. Ezért XBY és XCY háromszögek területe egyenlő, mert alapjuk (XY) és hozzá tartozó magasságuk (XY és BC párhuzamos egyenesek távolsága) is megegyezik. SBX háromszög területe úgy adódik, hogy XBY háromszög területéből kivonjuk YSX háromszög területét, SCY háromszög területe úgy adódik, hogy XCY háromszög területéből kivonjuk YSX háromszög területét. Mivel egyenlő területekből vonjuk ki ugyanazt a területet, ezért az eredmények is megegyeznek. Tehát SBX és SCY háromszögek területe egyenlő.
b) Mivel BY súlyvonal, ezért felezi az ABC háromszög területét. T1-et úgy kapjuk, hogy az ABC háromszög területének feléből kivonjuk T2-t, T3-at pedig úgy kapjuk, hogy az ABC háromszög területének feléből kivonjuk T4-et. Mivel T2=T4, ezért T1=T3, tehát SBC háromszög és AXSY négyszög területe megegyezik.
II. Megoldás: a) CX és BY súlyvonalak, metszéspontjuk a háromszög súlypontja, mely harmadolja a súlyvonalakat. SBX háromszög XB oldala tehát AB fele, az XB oldalhoz tartozó magassága pedig az ABC háromszög AB oldalához tartozó magasságának harmada, így SBX háromszög területe az ABC háromszög területének hatodrésze. Hasonlóan mutatható meg, hogy SCY háromszög területe is az ABC háromszög területének hatodrésze, így SBX és SCY háromszögek területe megegyezik.
b) Az SBC háromszög BC oldalhoz tartozó magassága harmada az ABC háromszög BC oldalhoz tartozó magasságának, tehát SBC háromszög területe az ABC háromszög területének harmadrésze. Az AXSY négyszög területét úgy kapjuk, hogy ABC háromszög területéből kivonjuk az AXSY négyszögön kívüli részek területét, ami összesen ABC háromszög területének 2/3 része. Tehát AXSY négyszög területe az ABC háromszög területének harmada, így megegyezik SBC háromszög területével.
Statistics:
154 students sent a solution. 6 points: 87 students. 5 points: 11 students. 4 points: 10 students. 3 points: 12 students. 2 points: 7 students. 1 point: 19 students. 0 point: 6 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, December 2005
