Problem K. 68. (January 2006)

K. 68. Connect an interior point of a parallelogram to each vertex. Show that it is possible to construct a quadrilateral with the four segments hence obtained as sides such that its vertices are lying on the sides of the parallelogram.

(6 pont)

Deadline expired on February 10, 2006.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás:

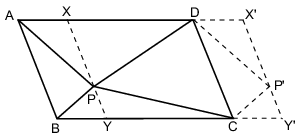
Használjuk az ábra jelöléseit! Fektessünk a P pontra a paralelogramma egyik oldalával párhuzamos egyenest, ez a paralelogramma megfelelő oldalait az X és Y pontokban metszi. Toljuk el az ABXY paralelogrammát AD-vel párhuzamosan úgy, hogy az A pont D-be kerüljön. Az eltolás során az X, P, Y, B pontok rendre az X', P', Y', C pontokba kerülnek át. Mivel AX=DX', ezért AD=XX'; továbbá AB=XY=DC=X'Y'. Ezek szerint a kapott XYY'X' paralelogramma az ABCD paralelogrammával egybevágó, hiszen a megfelelő oldalak párhuzamosak és egyenlők. Ebben a paralelogrammában a PCP'D négyszög éppen a PA, PB, PC, PD szakaszokból szerkesztett négyszög, melynek csúcsai a paralelogramma oldalain vannak. Ha az XYY'X' paralelogrammát visszatoljuk az ABCD paralelogrammába, akkor a PCP'D négyszög eltoltja éppen a keresett szerkesztendő négyszög.

Statistics:

130 students sent a solution.
6 points:	62 students.
5 points:	18 students.
4 points:	16 students.
3 points:	9 students.
2 points:	4 students.
1 point:	5 students.
0 point:	11 students.
Unfair, not evaluated:	5 solutionss.

Problems in Mathematics of KöMaL, January 2006