 Problem K. 73. (February 2006)
Problem K. 73. (February 2006)
K. 73. ABCD is a square of 5-cm sides. An equilateral triangle CDE is drawn outwards to the side CD. a) Find the angles of the triangle ABE. b) What is the radius of the circle that passes through all three vertices of triangle ABE?
(6 pont)
Deadline expired on March 10, 2006.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás:
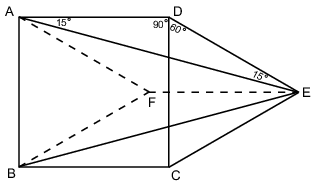
a) Az ADE szög 150o, mivel ADC szög 90o és CDE szög pedig 60o. Az ADE háromszög egyenlő szárú háromszög, ezért DAE szög nagysága 15o. Mivel BAD szög 90o, ezért BAE szög 75o. A szimmetria miatt ABE háromszög egyenlő szárú, tehát ABE szög is 75o-os. Így az AEB szög nagysága 30o.
b) Toljuk el a DCE háromszöget az ABF háromszögbe. Az eltolás 5 cm-en történt (a négyzet oldala mentén), így EF hossza 5 cm. Másrészt viszont az eltolt szabályos háromszög minden oldala szintén 5 cm hosszú, tehát az F pont 5 cm távolságra van A, B és E pontoktól. Ez azt jelenti, hogy az ABE háromszög minden csúcsa illeszkedik az F közepű, 5 cm sugarú körre. Tehát a keresett sugár hossza 5 cm.
Statistics:
176 students sent a solution. 6 points: 76 students. 5 points: 20 students. 4 points: 25 students. 3 points: 34 students. 2 points: 8 students. 1 point: 3 students. 0 point: 2 students. Unfair, not evaluated: 8 solutionss.
Problems in Mathematics of KöMaL, February 2006
