 |
A K. 79. feladat (2006. március) |
K. 79. Robi robot egy szobába van bezárva. Elindul egyenesen és megy, amíg falba nem ütközik. (Egy szobának csak a külső határvonal mentén lehetnek falai.) Ekkor jobbra fordul, és megy tovább. Ha nem tud jobbra fordulni, mert falba ütközne, balra fordul, és megy tovább. Ha nem tud sem jobbra, sem balra fordulni, akkor kikapcsolja magát.
Az 1. ábrán olyan szoba látható, melyben ha az 1-gyel jelölt helyről indul Robi, akkor miután körbejárja a szobát, oda is érkezik vissza, és ott leáll. A 2. ábrán olyan szoba látható, amelyben akár az 1-es, akár a 2-es helyről indul a robot, mindig a kiindulási helyre ér vissza, és ott leáll. A 3. ábrán az 1-es helyről a 2-esbe jut Robi, és ott leáll, míg a 2-esről az 1-esbe jut, és ott leáll. (Az ábrákon jelölt négyzetrács csak a tájékozódást segíti.)
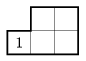
1. ábra
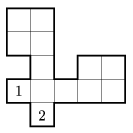
2. ábra
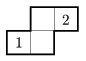
3. ábra
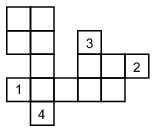
Rajzoljunk olyan szobát, ahol 4 kiindulási hely van: az 1-esből a 2-esbe jut, és ott leáll; a 2-esből a 3-asba jut, és ott leáll; a 3-asból az 1-esbe jut, és ott leáll; a 4-esből indulva ugyanoda érkezik vissza, és ott leáll.
(6 pont)
A beküldési határidő 2006. április 10-én LEJÁRT.
Megoldás: Például az alábbi szoba megfelel:
Statisztika:
109 dolgozat érkezett. 6 pontot kapott: 95 versenyző. 4 pontot kapott: 5 versenyző. 0 pontot kapott: 8 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2006. márciusi matematika feladatai

