 Problem K. 90. (September 2006)
Problem K. 90. (September 2006)
K. 90. The first nine positive integers can be written in the 9 fields bounded by the rings in the logo of the Olympic Games so that the sum of the numbers in each ring is 14. Such an arrangement is shown in the Figure. How can the numbers be arranged so that the sum is 13 in each ring? Find as many solutions as you can.
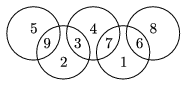
(6 pont)
Deadline expired on October 10, 2006.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás: Az öt karika mindegyikében az összeg 13, ez összesen 65, míg az első 9 számjegy összege 45. Tehát a négy metszetben a számok összege 20 kell legyen. Ez, valamint, hogy két számból csak háromféleképpen (9+4=7+6=8+5) lehet a 13-at összerakni, lecsökkentik a lehetőségek számát. Az összes lehetőséget kipróbálva ezt a két megoldást kapjuk:
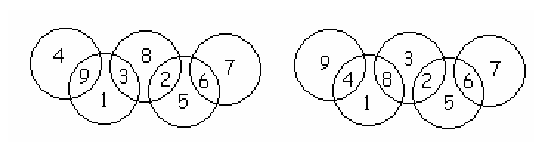
Statistics:
270 students sent a solution. 6 points: Bene Gergely, Bognár Barna, Dávid János, Fialowski Melinda, Garamszegi Balázs, Grőger Tímea, Gyebnár Zsófia, Hegedűs Csaba, Kovács 729 Gergely, Kovács Anita, Lajtai Krisztina, Lupsic Balázs, Márkus Rebecca Sheila, Mihálka Éva Zsuzsanna, Németh-Csóka Mihály, Pálinkó Márton, Pasztuhov Anna, Südi Anna, Székely Anna Krisztina, Sziráky Flóra, Tóth 004 Tamás, Tutor Gábor, Welsz Edit. 5 points: Galambos 124 Mónika, Gerlei Klára Zsófia, Tölgyesi Péter. 4 points: 7 students. 3 points: 41 students. 2 points: 75 students. 1 point: 107 students. 0 point: 11 students. Unfair, not evaluated: 3 solutionss.
Problems in Mathematics of KöMaL, September 2006
